案例解析：银行云柜员调度优化问题

量子计算与运筹优化的结合是当前量子技术应用的重要方向，其核心是利用量子计算的并行性优势解决经典计算难以高效处理的复杂优化问题，两者结合的研究可以显著提升人工智能、物流、金融等行业的决策效率，是量子计算最具商业价值的应用方向之一。

本节将以银行云柜员调度优化问题为例，讲述量子+运筹优化的结合应用。

场景介绍

云柜台专门服务由自助设备渠道接入的客户，客户点击接入按键后，系统会将用户自动分配至空闲柜员并开启连线，如果全部柜员繁忙没有空闲窗口，客户会自动进入等待队列。 云柜系统每月初会对当月每日值班人数进行排班，值班人数依据每月的忙期闲期制定，排班会限定每天可用的柜员人数上限。此外，需要安排每日的时间表，每日8:30-17:30为工作时间，每半小时为一个班次，需要指定该班次人员。

这是一个经典的M/M/1模型问题，M/M/1模型问题是排队论中最简单的一种模型。排队是一个运筹学知识概念，它是指一个单一服务台，顾客到达服从泊松分布，服务时间服从指数分布的排队系统。其中，M表示到达率和服务率都是指数分布，1表示只有一个服务台。

在M/M/1模型中，顾客到达率λ和服务率μ是两个重要的参数。到达率λ表示单位时间内到达系统的顾客数的期望值，服从参数为λ的泊松分布；服务率μ表示单位时间内一个顾客被服务完成的期望值，服从参数为μ的指数分布。假设顾客到达和服务时间是独立的，且服务时间服从无记忆性的指数分布，则该模型的稳态分析可以得到以下几个重要的性质：

• 平均队长L：系统中平均等待服务的顾客数；
• 平均逗留时间W：顾客在系统中逗留的平均时间；
• 平均服务时间S：一个顾客接受服务的平均时间；
• 系统利用率ρ：服务台被占用的时间比例；

这些性质可以通过使用稳态分析方法来计算，其中最常用的方法是利用平衡方程法。通过计算这些性质，可以对M/M/1模型进行评估和优化，以提高系统的效率和服务质量。

M/M/1模型虽然简单，但是在实际应用中有着广泛的应用，如电话交换系统、计算机网络、银行窗口等。因此，掌握M/M/1模型的基本原理和分析方法对于学习排队论和实际应用都具有重要意义。

泊松分布是一种离散概率分布，它描述了在一段时间内某个事件发生的次数，如一小时内接到的电话数、一天内发生的交通事故数等。泊松分布的概率密度函数为：

$$P(X=k)=\frac{{\lambda }^k\cdot e^{-\lambda }}{k!}$$

其中，$X$表示事件发生的次数，$k$表示具体的次数，$\lambda$表示单位时间内事件发生的平均次数，$e$表示自然对数的底数。

泊松分布的特点是：在一定时间内，事件发生的次数是独立的，且事件发生的概率相等。泊松分布的期望值和方差都等于λ，即：

$$E(X)=\lambda$$$$Var(X)=\lambda$$

需要注意的是，泊松分布只适用于事件发生的概率很小、事件之间是独立的、事件发生的平均次数是已知的情况。如果事件发生的概率很大，或者事件之间不是独立的，或者事件发生的平均次数是未知的，则泊松分布就不适用了。

一、假设条件

1. 云柜员没有工作效率高低之分；
2. 云业务没有办理时间长短之分。

二、决策变量

1. 每月1日决定该月各工作日的云柜员数量（不超过60）；每个工作日为月初分配到当日的云柜员安排工作时间，从早上8点半到下午5点半每半小时一档。每天总共是18个半小时长的时间档。
2. 第一阶段建模将每月1日决定该月各工作日的云柜员数量做为给定约束条件处理；第二阶段建模再考虑使用Benders decomposition进行每月1日和每个工作日两个层次的共同优化。

三、优化目标

1. 最小化当日客户平均等待时间的最大值（每个时间档都统计客户平均等待时间）；
2. 最小化云柜员的工时。

四、约束条件

1. 每位云柜员每个工作日的工作总时间最长为8小时（无须连续）；
2. 保证排队系统达到稳态，队伍长度不会持续增加，即云柜员数乘以云柜员服务率应大于客户到达率。

五、优化目标的数学定义

首先将问题描述成一个整数规划问题（IP），变量为某工作日21个时间档（8:30-19:00，每半小时一档）每个时间档分配的工时亦即云柜员数量。

注意：这里工时的定义跟一般工时的定义不一样。为了简化数学表达式，这里1个工时的定义是：1个工时=1位工人0.5小时。所以最小化总工时的优化目标可以表达为：

$$min\left(\sum _{i=1}^{21}{n}_i\right)=min(n_1+n_2+\cdots +n_{21})n_i\in {\mathbb{Z}}^{+}$$

另外我们可以使用每月1日决定该月各工作日的云柜员数量来表达每位云柜员每个工作日的工作总时间最长为8小时（即16个半小时）的约束：

$$\begin{array}{rl}& \sum _{i=1}^{21}{n}_i=n_1+n_2+\cdots +n_{21}\le 16N\\ & N_1\le n_1\le N\\ & N_2\le n_2\le N\\ & ⋮\\ & N_{21}\le n_{21}\le N\end{array}$$

其中$N_1,N_2,\cdots ,N_{21}$代表各时间档为保证排队系统达到稳态所需要的最少云柜员数量。

注意：这里使用了云柜员没有工作效率高低之分的假设条件，同时忽略了每位云柜员具体的排班时间。因为在该假设条件下每位云柜员的工时是不可区分（indistinguishable）的，虽然每位云柜员的身份是独一无二（distinct）的。

假定我们已知客户平均等待时间与云柜员数量和时间档的映射关系：

$$\begin{array}{rl}{t}_1& =f_1(n_1)\\ t_2& =f_2(n_2)\\ & ⋮\\ t_{21}& =f_{21}(n_{21})\end{array}$$

其中$t_1$为8:30到9:00时间档，$n_1$为分配到该时间档的云柜员数量；$t_2$为9:00到9:30时间档，$n_2$为分配到该时间档的云柜员数量；以此类推。用这个关系我们就可以构建最小化客户平均等待时间最大值的优化目标：

$$min(max(t_1,t_2,\dots ,t_{21}))$$

该问题有如下等价的线性规划表达式：

$$\begin{array}{rl}& minu\\ & t_1\le u\\ & t_2\le u\\ & ⋮\\ & t_{21}\le u\end{array}$$

整合以上各个优化目标和约束条件，我们得到如下云柜员调度优化问题的整数规划问题表达式：

$$\begin{array}{rl}& min(n_1+n_2+\cdots +n_{21})\\ & n_1+n_2+\cdots +n_{21}-16N\le 0\\ & n_1-N\le 0\\ & n_2-N\le 0\\ & ⋮\\ & n_{21}-N\le 0\\ & N_1-n_1\le 0\\ & N_2-n_2\le 0\\ & ⋮\\ & N_{21}-n_{21}\le 0\\ & minu\\ & t_1-u\le 0\\ & t_2-u\le 0\\ & ⋮\\ & t_{21}-u\le 0\end{array}$$

为了问题求解的便利，建议使用以下客户最大等待时间与云柜员数量和时间档的映射关系模板对客户最大等待时间进行统计概率分布拟合：

$$\begin{array}{rl}{t}_1& =f_1(n_1)=g_1-c{n}_1\\ t_2& =f_2(n_2)=g_2-c{n}_2\\ & ⋮\\ t_{21}& =f_{21}(n_{21})=g_{21}-c{n}_{21}\end{array}$$

该模板的好处是分离了客户最大等待时间对云柜员数量的依赖关系和客户最大等待时间对时间档的依赖关系，同时对云柜员数量的依赖关系是线性的。这里我们使用了第二个假设条件——云业务没有办理时间长短之分：常数$c$可以被认为是云业务的办理时间。

同时建议客户最大等待时间对时间档的依赖关系$g_i$使用整数目标域，这样可以便利对整数变量$n_1,n_2,\cdots ,n_{21}$的二进制编码（binary encoding）。

六、客户平均等待时间与云柜员数量的映射关系

通过观察客户到达速率的特征，发现客户流服从Poisson分布，柜员服务时间服从Erlang分布。通过观察业务处理模式，发现场景适用运筹学M/Er/R排队系统^[1]。在本例中，$R$为柜员人数。

根据运筹学稳态公式可直接求得顾客的平均等待时间，M/Er/R模型中顾客平均等待时间$W_q$存在近似公式，可以认为是 M/Er/1 模型中顾客平均等待时间$W_q^1$除以服务台数量$R$。^[1]发现同时存在一个更精确的近似公式，如下:

$$W_q^{<}(\rho ,R>1,k>1)\simeq f(\rho )\frac{\rho (1+1/k)}{2\mu (1-\rho )}$$

其中

$$f(\rho )=p_0\frac{R^R}{RR!}\cdot \frac{{\rho }^{R-1}}{1-\rho }$$

通过查表可知，${\rho }_0$约为 0.79，$\rho$为服务台的服务强度，每时段的服务强度${\rho }_i$可以通过统计分析得到。于是第$i$时刻客户平均等待时间为：

$$t_i=p_0\cdot \frac{n_i^{n_i}}{n_i{n}_i!}\cdot \frac{{\rho }_i^{n_i-1}}{1-{\rho }_i}\cdot \frac{1.25{\rho }_i}{2{\mu }_i(1-{\rho }_i)}$$

以下根据M/Er/R排队理论做举例计算：假设8:30时间档的云柜员人数为15，客户到达平均间隔时间为4.78秒，客户到达时间服从exponential分布，那么客户到达率为：

$$\lambda =\frac{1}{4.78}$$

假设云柜员全天服务时间均值约为25秒，方差150。用$X$代表服务时间，因此可得出：

$$k=\frac{\mathbb{E}[X]}{\text{Var}[X]}\approx 4$$

所以Erlang分布的系数为：

$${\mu }_0=\frac{k}{\mathbb{E}[X]}=0.16$$

假定该时间档整体服务率$\frac{1}{{\mu }_i}=\frac{1}{25}$。由此可得：

$${\rho }_i=\frac{{\mu }_i}{\lambda R}=\frac{25}{4.78\times 15}=0.35$$

将各参数带入以上客户平均等待时间公式计算可得：

$$t_i=0.79\cdot \frac{{15}^{15}}{15\cdot 15!}\cdot \frac{{0.35}^{14}}{1-0.35}\cdot \frac{1.25\cdot 0.35}{2\cdot (1/25)\cdot (1-0.35)}=0.06$$

需要指出的是，

1. 本公式建立的客户平均等待时间与云柜员数量的映射关系过于复杂，涉及柜员数的阶乘，不容易降阶；
2. 本公式的适用条件为$\rho \gg 0$，即服务强度大于0.5的情况下对平均服务时间的预测结果较准确，但是经过统计发现存在服务强度小于 0.5 的时间档，导致预测结果不准确；
3. 另一方面，在文献里很多作者把M/Er/R当作M/G/R的一个特殊形式。

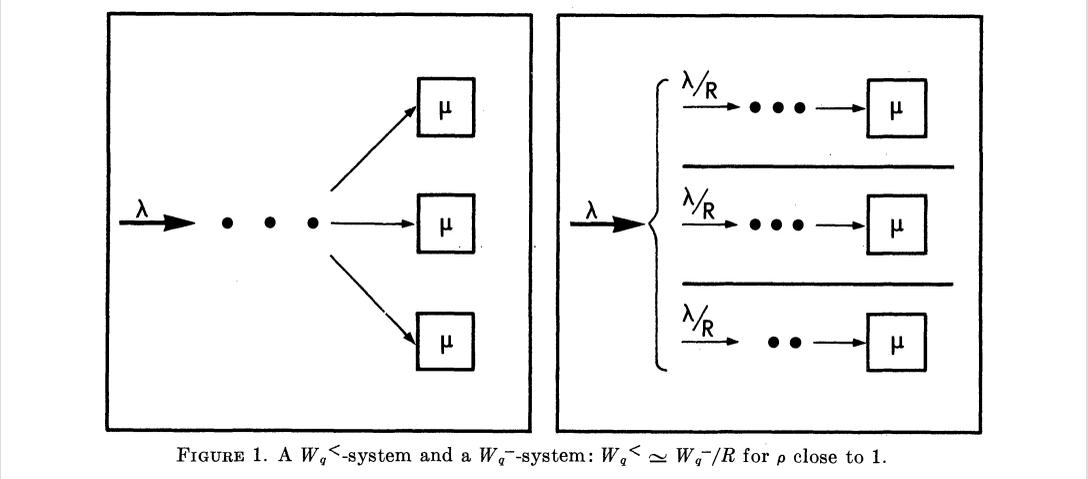
因此我们探索使用M/G/R排队理论来计算客户平均等待时间。该排队系统默认客户流服从Poisson分布，而服务率服从广义分布（general service-time distribution）。查阅 ^[2] 可知该系统稳态平均等待时间公式如下：

$$W(r_j,v)\simeq v^{2}W(r_j,1)+(1-v^2)W(r_j,0)$$

设定$r_i=1$，该公式与针对特殊情况的( M/$E_1$/r) 提出的公式一致，并且可以被视为波拉切克-欣钦（Pollaczek-Khintchine）公式的推广：

$$W(1,v)=\frac{\rho (1+v^2)}{2(1-\rho )\mu }=v^{2}W(1,1)+(1-v^2)W(1,0)$$

• 对于给定的$v$值，平均排队时间$W(r_j,v)$的任意值都可以用相对百分比误差来近似：$e=100\times \frac{\text{近似值}-\text{理论值}}{\text{理论值}}$，该误差根据涉及的参数值为正或负，且当$\rho \to 1$时趋于 0；对$r_j$的值不敏感，绝对值非常小，因此如果没有解析结果，很难被识别。
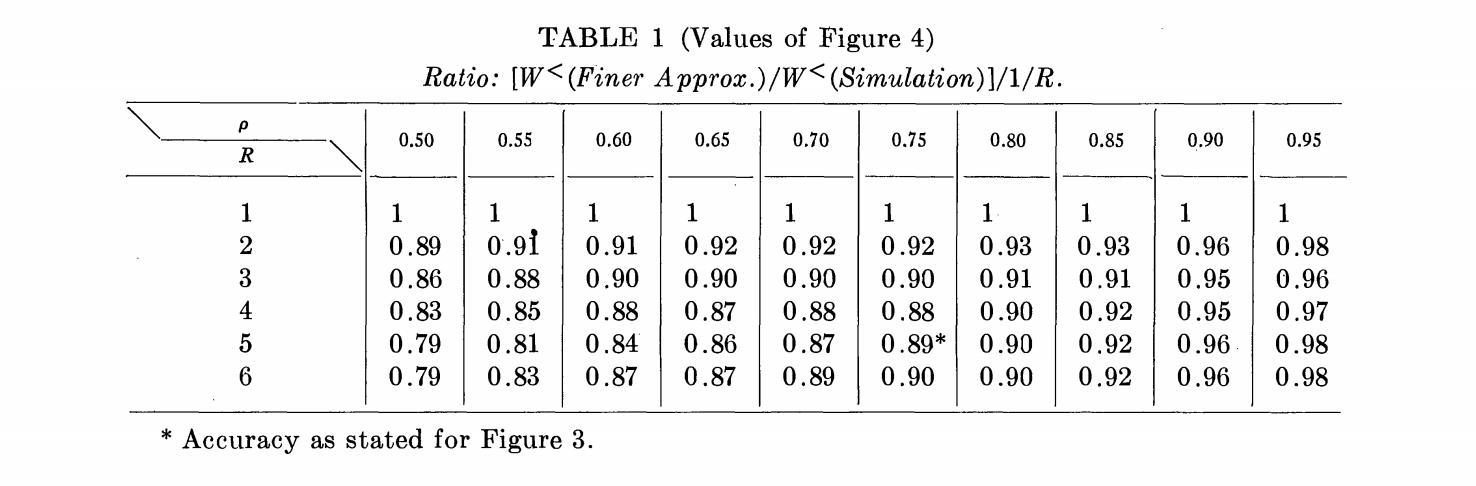
  作为$e$量级的一个示意，上方的表1给出了在过程( M/$E_2$/$r_j$）且$2\le r_j\le 6$，$\mu W(r_j,1/\sqrt{2})$ = 0.05, 0.10, 0.20, 0.50和1.00，中使用该公式评估平均排队时间时产生的相对百分比误差。

• $W(r_j,v)$的任意值都可以用相对百分比误差来近似，该误差如最初预期的那样随$v$变化：当$v$趋近于0或1时，误差趋于0，并且在中间某个位置达到最大绝对值。

从实际应用角度看，如果近似评估$W(r_j,0)$，该公式还可以进一步简化：

$$W(r_j,v)\simeq [\frac{1+v^2}{2}+\frac{(1-v^2)(1-\rho )(r_j-1)(\sqrt{(4+5r_j)}-2)}{16\rho r_j}]W(r_j,1)$$$$t_{\text{i}}=[\frac{1+v^2}{2}+(1-v^2)(1-{\rho }_i)(n_{\text{i}}-1)\frac{\sqrt{4+5n_{\text{i}}}-2}{16{\rho }_i{n}_{\text{i}}}]\cdot t_{\text{i}}^{M/M/n_{\text{i}}}$$$$t_{\text{i}}^{M/M/n_{\text{i}}}=\frac{L_{\text{s}}}{{\lambda }_{\text{i}}}-\frac{1}{{\mu }_{\text{i}}}=\frac{L_{\text{q}}+\rho }{{\lambda }_{\text{i}}}-\frac{1}{{\mu }_{\text{i}}}=\frac{\frac{p_0{\rho }^{n_{\text{i}}}{\rho }_{n_{\text{i}}}}{n_{\text{i}}!(1-{\rho }_{n_{\text{i}}}{)}^2}+\rho }{{\lambda }_{\text{i}}}-\frac{1}{{\mu }_{\text{i}}}$$$$p_0={[\sum _{n=0}^{r-1}\frac{{\rho }^{n_{\text{i}}}}{n_{\text{i}}!}+\frac{{\rho }^{n_{\text{i}}}}{n_{\text{i}}!(1-{\rho }_{n_{\text{i}}})}]}^{-1}$$$${\rho }_i=\frac{{\lambda }_{\text{i}}}{{\mu }_{\text{i}}}$$$${\rho }^{n_{\text{i}}}=\frac{{\lambda }_{\text{i}}}{n_{\text{i}}\cdot {\mu }_{\text{i}}}$$

其中${\rho }_i$依旧为第$i$时刻的服务强度，$n_i$依旧为第$i$时刻的云柜员数量，${\lambda }_i$和${\mu }_i$依旧为第$i$时刻的客户到达率和云柜员服务率，$v$为服务时间的变异系数，$t_i^{M/M/n_i}$为代入第$i$时刻参数M/M/r排队系统的平均等待时间。

注意到$t_i$是$n_i$非整数阶的函数，所以需要进一步近似。同时因为$n_i$可能是很小的整数，所以无法使用$(n_i-1)/n_i\approx 1$的近似。

七、数学建模

考虑到对M/G/R公式进行解析函数近似的难度。我们通过首先将$n_i=1,2,\dots ,60$带入以上M/G/R公式计算平均等待时间$t_i$，然后再以列表的方式而非解析函数形式定义$t_i$与$n_i$的映射关系，见如下表格所示：

n1	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40
t1	10000	10000	10000	10000	10000	432	135	55	24	10	4	2	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

请注意，表格中$t_i$的单位是百分之一秒，并且是对公式计算结果进行了四舍五入的结果。

为构建二元值变量从而将以上整数规划问题（IP）转化成二元值整数规划问题（BIP），我们定义$n_{ij}=j$，其中$i=1,2,\dots ,21$代表以上表格工作簿的个数，$j=1,2,\dots ,60$代表每个工作簿有60行的可选值（这里我们使用了在任一工作日都不会分配超过60位云柜员的业务信息）。同时定义$t_{ij}$为表格中的每一个工作簿的第二列即客户平均等待时间所组成的矩阵。

我们引入二元值变量$x_{ij}\in \{0,1\}$来表示第$i$个工作簿是否取了第$j$行的$n_i$和$t_i$数值。

则以上优化目标可以表示成如下形式：

公式	说明
$\sum _{j=1}^{60}{x}_{ij}=1$	保证每个工作簿必选且只选一个值
$min\sum _{i=1}^{21}\sum _{j=1}^{60}{n}_{ij}{x}_{ij}$	等价于以上的$min(n_1+n_2+\cdots +n_{21})$
$\sum _{i=1}^{21}\sum _{j=1}^{60}{n}_{ij}{x}_{ij}-16N\le 0$	等价于以上的$n_1+n_2+\cdots +n_{21}-16N\le 0$
$\sum _{j=1}^{60}{n}_{ij}{x}_{ij}-N\le 0$	等价于以上的$n_i-N\le 0$
$minu$	同上$u$，即最小化$t_1,t_2,\dots ,t_{21}$的最大值
$\sum _{j=1}^{60}{t}_{ij}{x}_{ij}-u\le 0$	保证$u$是$t_1,t_2,\dots ,t_{21}$的最大值

这个模型忽略各时间档为保证排队系统达到稳态所需要的最少云柜员数量的约束条件。其理由是我们可以通过对未满足该约束条件所带来的客户平均等待时间的增长的赋值来作为惩罚，从而以软约束的方式去满足这个约束条件。

目前在上述表格中，未达到稳态的惩罚时间为10000，超过稳态平均等待时间两个数量级，依实际优化效果可以进一步提高这一数值以增强惩罚效果。

八、参考文献

[1] Erik Maaløe, Approximation Formulae for Estimation of Waiting-Time in Multiple-Channel Queueing System, Management Science, Vol. 19, No. 6, Application Series, pp.703-710 (1973)

[2] George P. Cosmetatos, Some Approximate Equilibrium Results for the Multi-Server Queue (M/G/r), Operational Research Quarterly, Vol. 27, No. 3, Part 1, pp. 615-620 (1976)