基于相干光量子计算的车辆涂装序列优化问题
摘要:车辆涂装环节中的序列优化问题是汽车制造业中的重要研究方向,指通过对进入喷涂车间的车辆进行合理排序,在满足柔性生产的基础上,尽量减少喷枪颜色切换,从而实现降本增效。这一问题已被证明是NP-hard问题,经典计算机在多项式时间内无法求解。
本项目以最优车辆作业序列为目标构建QUBO模型,并使用相干光量子计算机进行求解。结果表明,相干光量子计算机不仅在毫秒级时间内完成求解,并且找到了优于使用经典求解器Gurobi及模拟退火算法的结果。
1. 项目描述
在汽车涂装过程中,当前后车身需要喷涂不同颜色时,喷头须重新调整并清洗,这一过程中会产生额外漆料的浪费及设备停工,造成生产成本显著上升,同时带来一定的空气污染问题。为降本增效、满足柔性生产需求,涂装车间希望最大限度地将相同颜色的车身排列在一起。然而,进入涂装车间的车身序列往往是由是上游车间的出车间序列决定的,上一车间的车身序列通常无法满足这一要求,因此需要对作业序列进行调整,这就产生了涂装车辆序列优化问题。
据测算,单次喷枪切色造成的漆料浪费价值约为40元人民币,一线车厂年产量200-300万台汽车,以平均每生产5辆汽车进行一次喷枪切色计算,仅漆料的浪费就高达约2000万元人民币。即使将切色频率降低10%,都可以带来至少数百万元人民币的成本下降。因此,车厂均投入大量资源研究车辆涂装序列的优化问题。
然而,这一问题已被证明是一个NP-hard问题,使用经典计算机无法在多项式时间内求解。目前业内多使用启发式算法、贪心算法等方法对涂装作业顺序进行优化。但这些方法受限于算力,很难覆盖大规模的车辆排序,并且难以跳出局部次优。如下表,对3种类型的6辆汽车进行排序,分别喷涂为蓝色和红色,使用贪婪搜索方法无法找到全局最优解。
| C1 | C2 | C1 | C2 | C3 | C3 | switch | |
|---|---|---|---|---|---|---|---|
| greedy | b | b | r | r | b | r | 3 |
| optimal | b | b | r | r | r | b | 2 |
而相干光量子计算机以光量子比特作为基本单位,模拟伊辛模型的演化过程(在数学上等价于QUBO),专用于求解大规模组合优化类问题,已被证实可有效求解NP-hard问题,并且具有相比经典计算指数级的加速优势和更高的最优解求解概率。本项目通过将车辆涂装序列优化问题建模为QUBO形式,并使用相干光量子计算机进行求解,不仅在毫秒级时间内求出最优解,同时找到相比经典计算更优的结果,为解决大规模车辆排序优化问题提供了一种新的求解思路。
2. 问题描述
问题:在给定的含有不同类型车辆的涂装序列中,用蓝色或红色对车辆进行喷涂。通过对进入涂装车间的车身序列进行调整和优化,尽量将相同颜色的车身排在一起,以减少喷枪清洗和涂料更换的频率,从而降低生产成本和提高生产效率。


目标:最小化喷枪颜色转换次数。
约束条件:
- 对于每种车型i,喷成蓝色或者红色的车辆数量是一定的;
- 车辆顺序不能变换。
3. 建模过程
假设我们总共有N辆车,我们定义一个决策变量
定义一个类型列表
目标:
约束:
4. 结果
选取100个不同规模的计算实例进行测试,这些实例的规模从20量子比特至100量子比特不等,对应实际汽车涂装场景中汽车数量(即20-100辆车)的序列。测试结果表明,针对每个实例,相干光量子计算机都在毫秒级时间范围内完成了求解,并且都找到了问题的最优解,即最优涂装序列。
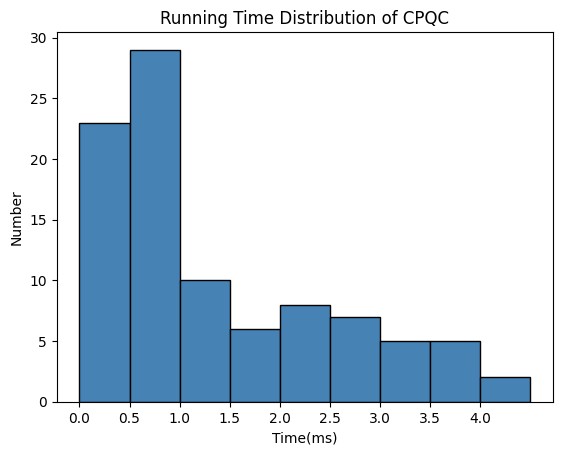
下图表示了100个计算实例的运行时间分布,我们可以看到,所有实例都在毫秒范围内找到了最优解。甚至超过75%的实例在不到1毫秒内完成了计算,即便是运行时间最长的计算也仍然在毫秒范围内。这种一致且快速的收敛凸显了使用相干光量子计算机求解的算法的效率和可靠性。
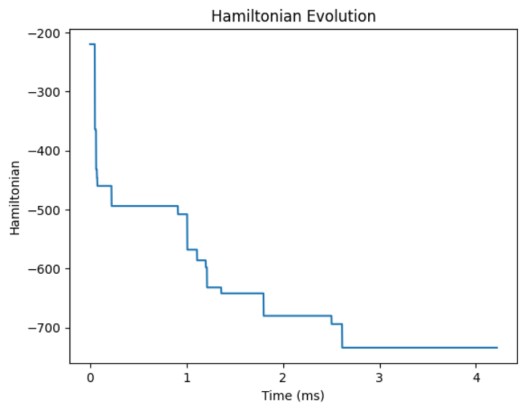
选取其中比特数最大的数据100_0.json为例,使用100量子比特相干光量子计算机求解,2.616毫秒完成求解。
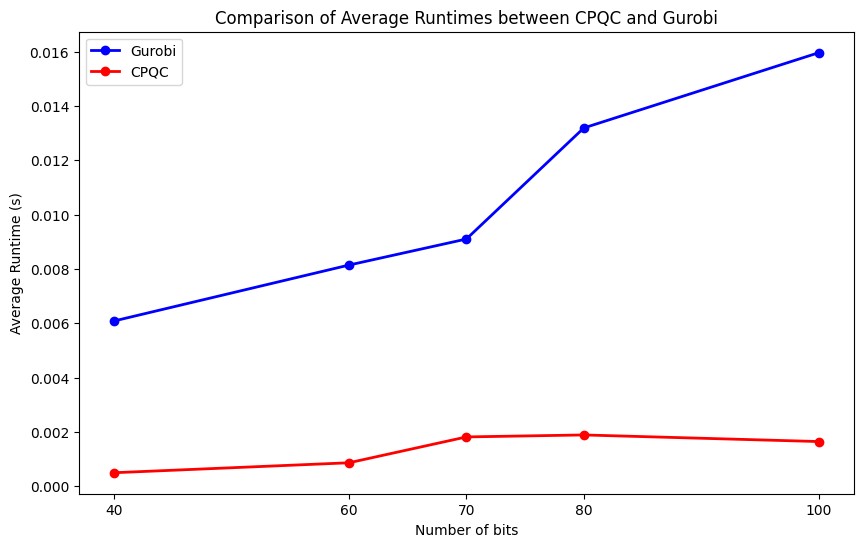
与经典优化求解器Gurobi进行对比:当处理40辆车的矩阵时,Gurobi求解器的运算时间大约需要6.08毫秒,相比之下,相干光量子计算机仅需要0.49毫秒。这一差距随着问题规模的扩大而变得更加显著:当矩阵规模扩展到100辆车时,Gurobi的运算时间增加到了16毫秒,而相干光量子计算机的运算时间仅为大约1.64毫秒。这也显示了相干光量子计算机的运行时间不受问题规模增加影响的潜在优势。
| # of cars/ms | 40 | 60 | 70 | 80 | 100 |
|---|---|---|---|---|---|
| Gurobi | 6.08 | 8.14 | 9.10 | 13.19 | 15.96 |
| CPQC | 0.49 | 0.85 | 1.81 | 1.84 | 1.64 |
5. 场景延展
该场景属于二元涂装问题(Binary Paint Shop Problem, BPSP),即每辆车的颜色只有蓝色或红色。相干光量子计算机基于量子比特进行计算,具备处理复杂的组合优化问题的能力,因此可以扩展到多颜色的涂装问题,即多元涂装问题(Multiple Paint Shop Problem, MPSP)。
喷涂车间的序列优化问题也可以被视为批量排列调度问题(Batch Permutation Scheduling Problem)的一个特殊案例,在理论上也属于NP-hard问题。它涉及到将一系列任务根据特定的顺序和约束进行安排,以优化某些性能指标,如减少总处理时间、降低成本或提高效率。这类问题在工业和制造业中有广泛的应用。以下是一些具体的应用场景:
生产调度:在制造业中,BPSP可以用来优化生产流程,确定不同产品的生产顺序,以减少设备调整时间和提高生产效率;
车辆路径规划:在物流和配送服务中,BPSP可以帮助规划车辆的送货顺序和路径,以减少行驶距离和时间;
维护调度:在设备维护和修理服务中,BPSP可以用于安排不同设备的维护顺序,以最小化停机时间和提高服务效率。
