论文精读：量子架构与混合技术驱动的统一稀疏优化方法

概要： 在技术飞速发展、数据洪流席卷全球的时代背景下，稀疏性已成为具有跨领域深远影响的关键特性。稀疏信号重构作为其重要应用，通过有限观测数据重建原始信号，在医学成像、通信系统和数据压缩等领域具有重大价值。然而传统稀疏信号重构方法常面临计算复杂度高的挑战，尤其在大规模问题上表现尤为突出。本文创新性地研究混合量子计算范式——相干伊辛机（CIM）在稀疏优化问题中的应用，通过在模型构建与实验验证两个维度的突破性贡献，提出了一种高效求解方案。我们所构建的模型通过显著降低计算资源需求并提升求解能力，实现了对现有方法的全面超越。研究还提供了关于模型性能保证的理论分析，为其可靠性与鲁棒性提供了理论支撑。为进一步增强模型的可扩展性与求解效率，我们引入Benders分解法将大规模问题拆解为更易求解的子问题。基于CIM平台的实验验证表明，该稀疏优化方法兼具高效性与精确性，为实际场景中复杂组合优化问题的求解开辟了新路径。

1. 研究背景

在信息科学快速演进的当下，人类正面临前所未有的数据洪流与高维复杂性挑战。在此背景下，“稀疏性”（sparsity）这一结构性特征因其高度信息压缩性，在图像处理、信号重建、特征选择、神经网络剪枝乃至医学成像等多个领域中扮演着核心角色，尤其是在观测数据受限、成本高昂或存储受限的情境中，稀疏优化技术提供了一种以最小代价提取最大信息的可能。因此，围绕稀疏结构展开的建模、重建与求解方法，已经成为了现代优化理论和应用实践的交汇焦点。

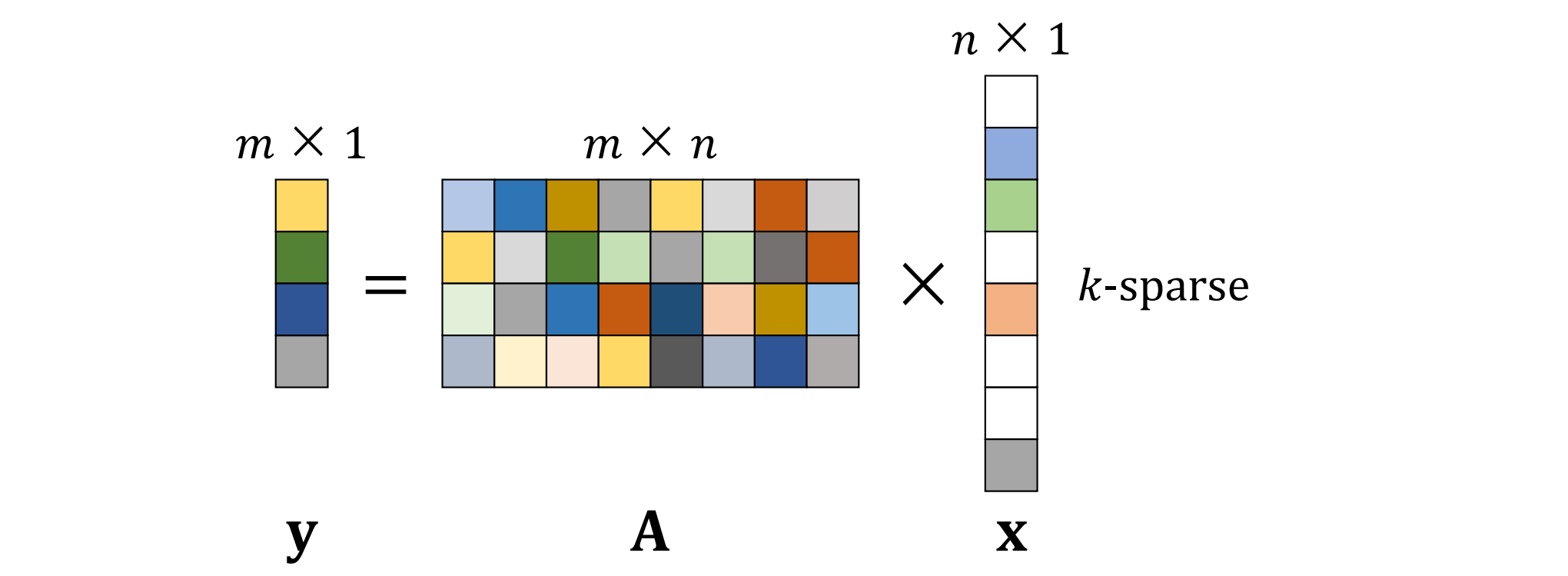
图1 稀疏优化领域中的一个具体实例——压缩感知问题的示意图，该图展示了一个高维稀疏信号到低维测量空间的转换过程

然而，尽管经典压缩感知（Compressed Sensing）理论为稀疏信号重建提供了坚实的理论基石，并通过对${\ell }_0$-范数与${\ell }_1$-范数之间的替代关系构建了诸多高效算法体系，但本质上，精确的稀疏度最小化问题仍然属于NP-难问题，难以通过多项式时间手段直接求解。传统求解策略或采用凸松弛（如LASSO）引入偏差，或依赖贪婪算法（如OMP）导致局部最优，尤其在处理大规模、高耦合结构时表现出明显的计算瓶颈。因此，寻求新的架构与范式，突破计算能力的限制，成为当前稀疏优化研究的关键命题。

与此同时，量子计算的发展为组合优化问题带来新机会，尤其是“近似量子硬件”（如D-Wave的量子退火器与本文重点关注的相干伊辛机CIM），为以低比特表示形式求解复杂QUBO（Quadratic Unconstrained Binary Optimization）问题提供了可能。CIM 作为一种基于光学器件（如退化光学参量振荡器）的模拟量子系统，不仅能够原生地映射Ising模型，还支持高度连接的变量网络，因而成为当前量子优化研究中最具工程可行性的候选之一。

基于这一背景，Wenxin Li等人（2025）提出了一种以CIM为求解器的统一稀疏优化框架，系统性地将三类典型的稀疏优化问题（${\ell }_0$正则、$k$-稀疏约束、不动稀疏度）转化为适用于量子硬件求解的QUBO问题，并提出了多种模型结构——基于混合变量表示的Model 1、降低比特数的Model 2.1与适用于固定稀疏度的Model 2.2。在建模之外，该工作还巧妙引入了Benders分解作为优化策略，实现了量子与经典模块的解耦与协同。本文还在CIM真实平台上完成了实验验证，展示了在几十到上百比特下的毫秒级求解性能。

2. 稀疏优化的经典框架回顾

在稀疏信号恢复（sparse signal recovery）问题中，核心挑战是如何在观测维度远小于信号维度的前提下，从有限的观测中准确估计原始信号。这一问题通常可以形式化为一个欠定线性系统：

$$\mathbf{y}=\mathbf{Ax},$$

其中$\mathbf{y}\in {\mathbb{R}}^m$是观测向量，$\mathbf{A}\in {\mathbb{R}}^{m\times n}$是观测矩阵，$\mathbf{x}\in {\mathbb{R}}^n$是待恢复的稀疏信号，且满足$m\ll nm\ll n$。稀疏性假设要求$\mathbf{x}$至多只有$k$个非零分量，即$\mathbf{x}$为$k$-稀疏的。根据Donoho等人的研究，如果观测矩阵$\mathbf{A}$满足受限等距性质（RIP），即其常数${\delta }_{2k}<1$，则稀疏解具有唯一性。最理想的模型是直接最小化${\ell }_0$-范数以寻找最稀疏的解：

$$\begin{array}{rl}\underset{\mathbf{x}\in {\mathbb{R}}^n}{min}& \parallel \mathbf{x}{\parallel }_0\\ \text{s.t.}& \mathbf{Ax}=\mathbf{y}\end{array}$$

该模型是NP-Hard的，因而在实践中难以直接求解。为此，研究者发展出三类更具实用性的问题变形，其定义如下：

• Definition 1（${\ell }_0$ 正则化的最小二乘问题）： 设$\mathbf{A}\in {\mathbb{R}}^{m\times n}$为测量矩阵，$\mathbf{y}\in {\mathbb{R}}^m$为观测向量，目标是在如下模型中求解稀疏向量$\mathbf{x}\in {\mathbb{R}}^n$：

$$\underset{\mathbf{x}\in {\mathbb{R}}^n}{min}\parallel \mathbf{Ax}-\mathbf{y}{\parallel }_2^2+\lambda \parallel \mathbf{x}{\parallel }_0$$

该问题常被称为${\ell }_0$-正则化的压缩感知模型或稀疏回归模型，结合了最小二乘残差与稀疏性惩罚两部分。在统计学中，这一模型对应于带惩罚项的回归建模，强调预测精度；而在反问题理论中，更强调信号系数的物理含义恢复，其思想在于在最小残差基础上鼓励稀疏解。由于直接优化$\parallel x{\parallel }_0$过于困难，很多文献采用${\ell }_1$-范数替代，形成凸松弛模型，如LASSO或Basis Pursuit Denoising（BPDN）。

• Definition 2（$k$-稀疏约束问题）： 相比正则化模型，部分应用中可直接给定最大稀疏度$k$，构成如下约束优化问题：

$$\begin{array}{rl}\underset{\mathbf{x}\in {\mathbb{R}}^n}{min}& \parallel \mathbf{Ax}-\mathbf{y}{\parallel }_2^2\\ \text{s.t.}& \parallel \mathbf{x}{\parallel }_0\le k\end{array}$$

这一形式常见于统计学习中的特征选择任务（feature selection），亦可用于机器学习模型的剪枝（如神经网络中通道或连接的筛除），在特征选择任务中尤为常见。典型形式如下：

$$\begin{array}{rl}\underset{w\in {\mathbb{R}}^p}{min}& \sum _{i=1}^n\ell (y_i,w^T{x}_i)\\ \text{s.t.}& \parallel w{\parallel }_0\le k,\end{array}$$

其中$\ell (\cdot )$是一个凸损失函数，如常见的平方损失$\ell (y,u)=\frac{1}{2}(y-u{)}^2$。该模型通过硬性限制最多使用 $k$个特征参数$w_j$，因此在模型可解释性、泛化能力与计算资源受限场景中具有广泛应用。此类问题虽然表达更直接，但由于约束空间是非凸的离散集合，所以计算起来依然复杂。

• Definition 3（固定稀疏度问题）： 当系统已知稀疏度恰为$k$，则问题可进一步强化为：

$$\begin{array}{rl}\underset{\mathbf{x}\in {\mathbb{R}}^n}{min}& \parallel \mathbf{Ax}-\mathbf{y}{\parallel }_2^2\\ \text{s.t.}& \parallel \mathbf{x}{\parallel }_0=k\end{array}$$

与Definition 2相比，该模型在稀疏度控制上更严格，适用于如通信系统中的码字选择、子载波分配或精确特征数量控制等场景。其可行域是${\mathbb{R}}^n$中稀疏度为$k$的向量集合，维度组合极其庞大，因而更具挑战性。上述三种模型构成了稀疏优化理论的基本范式，也对应了不同的数学结构与算法机制。

在方法层面，主流解决策略可以划分为三类：

• 凸松弛法：以${\ell }_1$-范数替代${\ell }_0$进行凸化处理。其代表为Basis Pursuit、LASSO等。该类方法可用标准优化工具求解，适合大规模问题，但在某些噪声或非高斯场景下存在性能瓶颈。
• 贪婪法：如OMP、CoSaMP、Stagewise Regression等，强调逐步筛选显著变量，虽然效率较高，但容易陷入次优。
• 贝叶斯方法：将稀疏性视为先验分布进行后验推断，典型如Sparse Bayesian Learning（SBL）方法，其性能较优，但计算复杂度高。 尽管上述方法已广泛用于工程实践，但在追求精确解或处理超大规模数据时，其理论限制仍不可忽视。尤其是在直接处理${\ell }_0$的原始形式时，传统方法往往需要高复杂度启发式搜索或混合整数编程，导致实际计算代价难以接受。

3. QUBO建模框架与CIM适配性

3.1 稀疏优化问题的QUBO表示：统一模型（Model 1）

稀疏优化问题本质上是一个包含非凸非线性项的组合优化问题，这类问题在传统算法体系中极度依赖启发式结构或连续松弛技术。而近年来快速发展的量子优化硬件，尤其是相干伊辛机（Coherent Ising Machine, CIM），为求解这一类问题提供了全新的物理实现路径。CIM 通过光学物理系统近似求解伊辛模型的能量极小化问题，而伊辛模型又可与二次无约束二进制优化（Quadratic Unconstrained Binary Optimization, QUBO）问题一一对应，构成“物理问题–计算模型–应用问题”的闭环。QUBO问题定义如下：

$$\underset{x\in \{0,1{\}}^n}{min}{x}^{\mathrm{\top }}Qx,$$

其中$Q$是对称的$n\times n$权重矩阵，$x$是由$0-1$二值变量构成的向量。它等价于无磁场下的伊辛模型最小化问题：

$$\underset{\sigma \in \{-1,+1{\}}^n}{min}-\sum _{i<j}{J}_{ij}{\sigma }_i{\sigma }_j,$$

通过变量替换$x_i=\frac{1}{2}(1+{\sigma }_i)$可实现从QUBO到伊辛模型的变换。该结构在CIM这类基于耦合光学振荡器网络的物理设备上可以高效求解，具有高并行性和天然的全连接能力，尤其适用于密集耦合问题。

本文首先提出了一种统一稀疏优化模型（Model 1），该模型设计的基本思路是在变量表达层引入混合结构：实数变量用于表示信号幅值，二值变量用于表示稀疏结构，保留了原始信号的数值精度，又为稀疏性表达与硬件实现提供了二进制嵌入空间。令$x=(x_1,x_2,\dots ,x_n)\in {\mathbb{R}}^n$为原始信号，每个$x_i$通过一个长度为$K$的二进制编码向量${\delta }_i\in \{0,1{\}}^K$映射得到：

$$x_i=g({\delta }_i),$$

其中 $g:\{0,1{\}}^K\to \mathbb{R}$是某种定点函数（如加权求和、带符号二进制扩展等）。同时，为表示稀疏性，引入三类二值变量，其中$z_i$表示$x_i=0$，即该分量是否为零；$z_i^{+}$、$z_i^{-}$则分别表示$x_i>0$和$x_i<0$的指示变量。为保证三者互斥且完备，需满足：

$$z_i^{-}+z_i+z_i^{+}=1,$$

并通过如下约束强制$x_i$在不同情况下取值于指定区间：

$$x{z}_i^{-}+ϵz_i^{+}\le x_i\le \overline{x}{z}_i^{+}-ϵz_i^{-},$$

其中$ϵ>0$是非零信号分量的最小幅值。为了确保$z_i^{-}$和$z_i^{+}$不同时为1，引入惩罚项$z_i^{-}\cdot z_i^{+}$加入到目标函数中。最终，整个优化问题被嵌入为如下QUBO表达形式：

$$\begin{array}{rl}H& =\sum _{i=1}^n(z_i^{-}+z_i^{+})\\ & +\lambda \sum _{\ell =1}^m{(\sum _{i=1}^n{A}_{\ell i}g({\delta }_i)-y_{\ell })}^2\\ & +\lambda \sum _{i=1}^n{z}_i^{-}{z}_i^{+}\\ & +\lambda \sum _{i=1}^n{[x{z}_i^{-}+ϵz_i^{+}+s_i^{(1)}-g({\delta }_i)]}^2\\ & +\lambda \sum _{i=1}^n{[\overline{x}{z}_i^{+}-ϵz_i^{-}-s_i^{(2)}-g({\delta }_i)]}^2,\end{array}$$

其中$s_i^{(1)},s_i^{(2)}$为辅助松弛变量，其本身可用额外二进制变量表示。可以看到，该模型虽然变量量较多，但形式统一，兼容了稀疏指示、信号表达和目标优化三类结构，非常适合后续分解算法与量子实现。

3.2 Quantum Benders分解算法

为解决稀疏优化问题中大规模二进制变量与连续变量混合所带来的复杂性，本文引入 Quantum Benders Decomposition 方法，将${\ell }_0$-范数优化问题重写为两阶段结构，分别处理离散选择与连续优化两类变量，从而实现经典-量子混合求解。

该问题被改写为如下形式：

$$\begin{array}{rl}\underset{\mathbf{x},\mathbf{z}}{min}& {\mathbf{p}}^{\mathrm{\top }}\mathbf{z}\\ \text{s.t.}& \mathbf{A}\mathbf{x}=\mathbf{b}\\ & \mathbf{B}\mathbf{x}+\mathbf{C}\mathbf{z}\le \mathbf{h}\\ & \mathbf{x}\in {\mathbb{R}}^n,\mathbf{z}\in \{0,1{\}}^{2n}\end{array}$$

其中$z=[z_1^{-},z_2^{-},\dots ,z_n^{-},z_1^{+},\dots ,z_n^{+}]$，表示稀疏结构，$p^{\mathrm{\top }}z=\sum _i(z_i^{-}+z_i^{+})$表示对非零元素的惩罚目标，$\mathbf{B}$、$\mathbf{C}$、$\mathbf{h}$分别为：

$$\mathbf{B}=\left[\begin{array}{c}-\mathrm{diag}\left({\mathbf{1}}_n\right)\\ \mathrm{diag}\left({\mathbf{1}}_n\right)\\ {\mathbf{0}}^{n\times n}\end{array}\right],\mathbf{C}=\left[\begin{array}{cc}\mathrm{diag}(\underset{―}{x}\cdot {\mathbf{1}}_n)& \mathrm{diag}(\epsilon \cdot {\mathbf{1}}_n)\\ \mathrm{diag}(\epsilon \cdot {\mathbf{1}}_n)& -\mathrm{diag}(\overline{x}\cdot {\mathbf{1}}_n)\\ \mathrm{diag}\left({\mathbf{1}}_n\right)& \mathrm{diag}\left({\mathbf{1}}_n\right)\end{array}\right],\mathbf{h}=\left[\begin{array}{c}{\mathbf{0}}^{2n\times 1}\\ {\mathbf{1}}^{n\times 1}\end{array}\right]$$

该结构明确划分了离散变量$\mathbf{z}$的选择行为（支持集生成）与连续变量$\mathbf{x}$的数值重构行为。因而Benders分解适用于此结构：将$\mathbf{z}$固定为支持结构，转化为子问题求解$\mathbf{x}$，再据其可行性与最优性反馈对主问题进行更新。

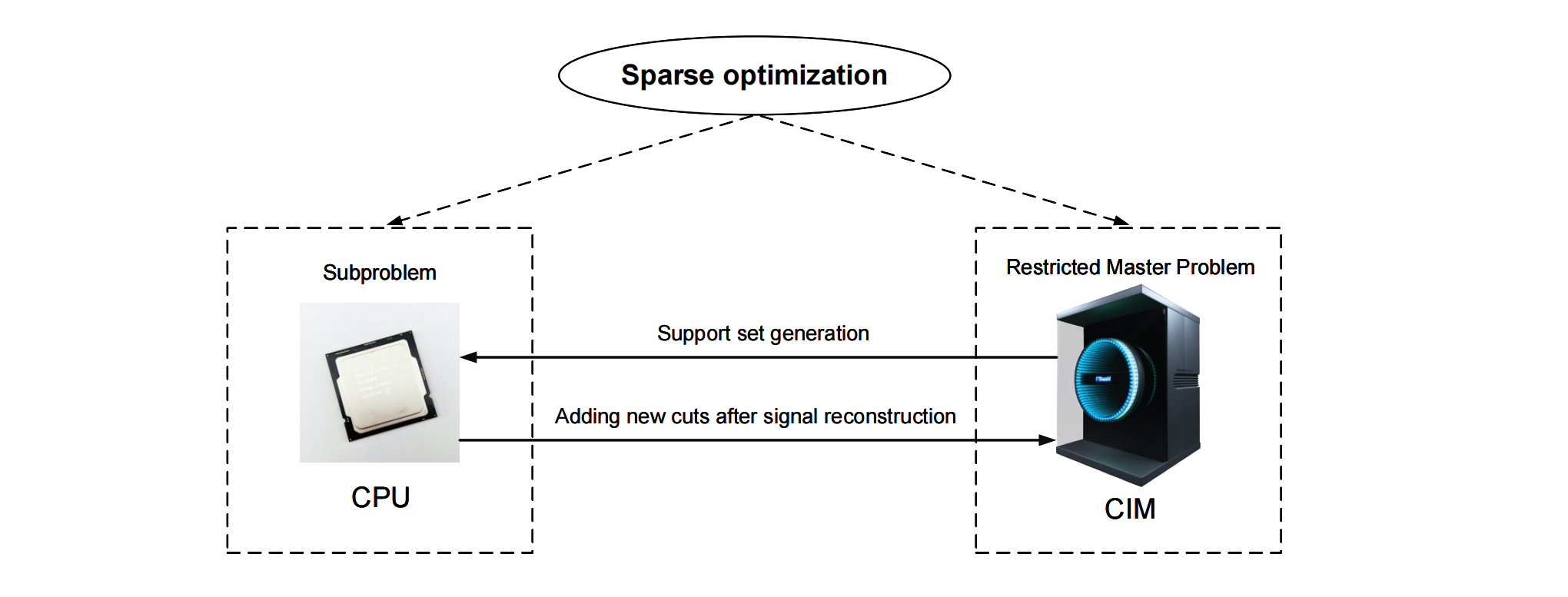
图2 面向稀疏优化的量子Benders分解算法流程，其中限制主问题(RMP)通过相干伊辛机(CIM)求解以生成支撑集，而子问题则在经典CPU端处理，基于重构信号生成新切割平面以迭代优化解。

在此框架下，主问题被重写为：

$$\underset{\mathbf{z}}{min}{\mathbf{p}}^{\mathrm{\top }}\mathbf{z}+t$$

其中 $t$ 表示对应于当前 $\mathbf{z}$ 所定义支持集下子问题的最优目标值，定义为：

$$\text{（原始子问题）}t=\underset{\mathbf{x}}{min}\left\{0\right|\mathbf{A}\mathbf{x}=\mathbf{b},\mathbf{B}\mathbf{x}\le \mathbf{h}-\mathbf{C}\mathbf{z}\}$$

$t=0$表示当前支持集下存在可行解$x$；若 $t=\mathrm{\infty }$，则说明该支持结构下无解。该子问题可进一步转化为对偶形式：

$$\begin{array}{rl}\text{（对偶子问题）}t=\underset{\lambda ,\nu }{max}& -{\lambda }^{\mathrm{\top }}\mathbf{b}-{\nu }^{\mathrm{\top }}(\mathbf{h}-\mathbf{C}\mathbf{z})\\ \text{s.t.}& {\mathbf{A}}^{\mathrm{\top }}\lambda +{\mathbf{B}}^{\mathrm{\top }}\nu =0\\ & \nu \ge 0\end{array}$$

该对偶问题有两种可能：

(1) 可行但无界（极射线）：存在$({\lambda }_i^{†},{\nu }_i^{†})$使得：

$${\lambda }_i^{†\mathrm{\top }}\mathbf{b}+{\nu }_i^{†\mathrm{\top }}(\mathbf{h}-\mathbf{C}\mathbf{z})<0$$

则对偶目标趋于 $-\mathrm{\infty }$，对应原始问题无解，需添加可行性割：

$${\lambda }_i^{†\mathrm{\top }}\mathbf{b}+{\nu }_i^{†\mathrm{\top }}(\mathbf{h}-\mathbf{C}\mathbf{z})\ge 0$$

(2) 存在最优极点：存在$({\lambda }_j^{‡},{\nu }_j^{‡})$，使得：

$$t={\lambda }_j^{‡\mathrm{\top }}\mathbf{b}+{\nu }_j^{‡\mathrm{\top }}(\mathbf{h}-\mathbf{C}\mathbf{z})$$

则添加最优性割：

$$t\ge {\lambda }_j^{‡\mathrm{\top }}\mathbf{b}+{\nu }_j^{‡\mathrm{\top }}(\mathbf{h}-\mathbf{C}\mathbf{z})$$

通过迭代添加上述割，Benders分解采用延迟约束生成策略构造主问题的松弛版本：

$$\begin{array}{rl}\text{（受限主问题 RMPₖ）}\underset{\mathbf{z},t}{min}& {\mathbf{p}}^{\mathrm{\top }}\mathbf{z}+t\\ \text{s.t. }& {\lambda }_i^{†\mathrm{\top }}\mathbf{b}+{\nu }_i^{†\mathrm{\top }}(\mathbf{h}-\mathbf{C}\mathbf{z})\ge 0,i\in {\mathcal{I}}_k\\ & t\ge {\lambda }_j^{‡\mathrm{\top }}\mathbf{b}+{\nu }_j^{‡\mathrm{\top }}(\mathbf{h}-\mathbf{C}\mathbf{z}),j\in {\mathcal{J}}_k\end{array}$$

最终，为将RMPₖ嵌入到CIM可求解的QUBO框架中，需引入slack variables并进行量子化编码，得到如下二次目标形式：

$$\begin{array}{rl}\underset{\mathbf{z},t}{min}& {\mathbf{p}}^{\mathrm{\top }}\mathbf{z}+\sum _i{2}^i{t}_i\\ & +\sum _{i\in {\mathcal{I}}_k}{({\lambda }_i^{†\mathrm{\top }}\mathbf{b}+{\nu }_i^{†\mathrm{\top }}(\mathbf{h}-\mathbf{C}\mathbf{z})-\sum _{\ell }{s}_{i\ell }^{(1)}\cdot 2^{\ell })}^2\\ & +\sum _{j\in {\mathcal{J}}_k}{(t+\sum _{\ell }{s}_{j\ell }^{(2)}\cdot 2^{\ell }-{\lambda }_j^{‡\mathrm{\top }}\mathbf{b}-{\nu }_j^{‡\mathrm{\top }}(\mathbf{h}-\mathbf{C}\mathbf{z}))}^2\end{array}$$

其中 $s_{i\ell }^{(1)}$、$s_{j\ell }^{(2)}$为slack variables的二进制表示，$t_i$为目标值$t$的量化比特。所有项均为二次形式，满足QUBO的嵌入要求。该算法流程如图2所示，降低了单次优化所需的变量数，使得量子求解器能处理更大规模问题：

伪代码：Quantum Benders分解算法

3.3 简化模型：稀疏优化的结构压缩与变量精简

在前述模型构建中（特别是Model 1与基于Benders分解的策略），为了表达${\ell }_0$稀疏性，模型引入了大量辅助变量（如正负符号指示、稀疏性判别变量、松弛变量等），虽然理论表达力强，但二进制变量数与问题规模成倍增长，导致实际量子硬件实现门槛高、耦合矩阵复杂、收敛路径不稳定。为此，文章提出一个更为精简的建模方案，构造逻辑直接作用于稀疏性判定变量$z_i$与二进制编码${\delta }_{ij}$的交互之上，构造了逻辑约束的变体，从而避免显式引入符号变量与大规模乘积项。

设每个变量$x_i$通过$K$个二进制变量${\delta }_{ij}$编码，编码函数为$x_i=g({\delta }_i)$，其中$g:\{0,1{\}}^K\to \mathbb{R}$，我们设定其唯一零点为${\delta }_0$，即$g({\delta }_0)=0$。为判定$x_i=0$的条件是否成立，构造以下逻辑约束：

• 若${\delta }_{ij}\in {\mathcal{I}}_0$（即${\delta }_j^{(0)}=0$），当${\delta }_{ij}=1$时说明$x_i\ne 0$；
• 若${\delta }_{ij}\in {\mathcal{I}}_1$（即${\delta }_j^{(0)}=1$），当${\delta }_{ij}=0$时说明$x_i\ne 0$。

因此，采用如下逻辑约束统一编码：

$$\begin{gathered} z_i\ge {\delta }_{ij},j\in {\mathcal{I}}_0 \\ {z}_i\ge 1-{\delta }_{ij},j\in {\mathcal{I}}_1 \end{gathered}$$

这类逻辑表达可以通过惩罚项加入QUBO表达式，从而显式编码逻辑判断。最终得到的Hamiltonian表达式如下：

$$H=\sum _{\ell =1}^m{(\sum _{i=1}^n{A}_{\ell i}\cdot g({\delta }_i)-y_{\ell })}^2+\lambda \sum _{i=1}^n{z}_i+\lambda \cdot H_0$$

其中补充项$H_0$表达为：

$$H_0=\sum _{i=1}^n[\sum _{j\in {\mathcal{I}}_0}({\delta }_{ij}-z_i{\delta }_{ij})+\sum _{j\in {\mathcal{I}}_1}(1-z_i)(1-{\delta }_{ij})]$$

该表达兼顾逻辑判定与量子实现能力，避免高阶项并可写成QUBO二次型。对于编码函数$g$，若设为线性函数：

$$g({\delta }_i)={\mathbf{w}}^{\mathrm{\top }}{\delta }_i+w_0$$

则可写为：

$${\mathbf{x}}^{\mathrm{\top }}={\delta }^{\mathrm{\top }}({\mathbf{I}}_n\otimes \mathbf{w})+w_0\cdot {\mathbf{1}}_n^{\mathrm{\top }}$$

从而整个目标函数可写为：

$$H={\mathbf{p}}^{\mathrm{\top }}{\mathbf{Q}}_2\mathbf{p}$$

其中$\mathbf{p}=[z^{\mathrm{\top }},{\delta }^{\mathrm{\top }}{]}^{\mathrm{\top }}\in \{0,1{\}}^{n(K+1)}$，${\mathbf{Q}}_2$为标准QUBO矩阵。该模型在正负值信号与非负值信号两类编码中均可适配：

• 示例 1（实值信号） 编码为：

$$x_i=2\overline{x}(\sum _{j=1}^K{2}^{-j}{\delta }_{ij}-0.5)\in [-\overline{x},\overline{x})$$

则对应稀疏逻辑条件为：

$$z_i\ge 1-{\delta }_{i1},z_i\ge {\delta }_{ij},j\ge 2$$

目标函数为：

$$\sum _{\ell }{(2\sum _i{A}_{\ell i}\overline{x}(\sum _j{2}^{-j}{\delta }_{ij}-0.5)-y_{\ell })}^2+\lambda \sum _i[(1-z_i)(1-{\delta }_{i1})+\sum _{j=2}^K({\delta }_{ij}-z_i{\delta }_{ij})]+\lambda \sum _i{z}_i$$

• 示例 2（非负信号） 编码为：

$$x_i=\overline{x}\sum _{j=1}^K{2}^{-j}{\delta }_{ij}\in [0,\overline{x})$$

逻辑条件统一为$z_i\ge {\delta }_{ij},\mathrm{\forall }j$，目标函数为：

$$\sum _{\ell }{(\sum _i{A}_{\ell i}\overline{x}\sum _j{2}^{-j}{\delta }_{ij}-y_{\ell })}^2+\lambda \sum _i\sum _j({\delta }_{ij}-z_i{\delta }_{ij})+\lambda \sum _i{z}_i$$

3.4 QUBO模型中的惩罚项$\lambda$设置

上述模型的优化效果显著依赖于惩罚项（正则项）系数数$\lambda$的选择。$\lambda$的作用可视为在数据拟合项与稀疏性约束项之间进行权衡：

• $\lambda$过小时，模型更接近普通最小二乘；
• $\lambda$过大时，所有$x_i$被压缩为0，导致欠拟合；
• 最优$\lambda$位于中间区域，保证模型可恢复原始稀疏结构。 然而，在量子优化（尤其是Ising物理实现）中，惩罚项的尺度过高将导致权重矩阵数值过大，从而在有限精度下产生显著干扰。为此，需要设置$\lambda$的下界，确保若解违反约束，则惩罚项带来的损失高于数据项的减益。在Ising模型中，目标为最小化：

$$\underset{{\sigma }_i\in \{-1,1\}}{min}{\sigma }^{\mathrm{\top }}J\sigma$$

若将第$i$个变量翻转，能量变化为：

$$\mathrm{\Delta }E=-4\cdot {\sigma }_i\cdot ⟨\sigma ,J_i⟩$$

其中$J_i$是第$i$行，$⟨\cdot ,\cdot ⟩$为内积。我们可通过规范化$\underset{A_{ij}\ne 0}{min}{A}_{ij}^2=1$，使得违反逻辑约束带来的代价大于最小可能减能项，因此设：

$${\lambda }_{min}=\underset{i}{max}\sum _j|J_{ij}|\cdot 4$$

这样设置后，能够确保约束的“逻辑惩罚项”在能量演化中占据主导，保证解不因违反逻辑而被误导至低能态。

4. 稀疏约束优化：从不等式控制到等式精确化

在完成了QUBO框架下稀疏建模的基本构建之后，本章进一步探讨如何在该模型体系中处理更复杂的稀疏约束形式，比如说问题2（$k$-sparse 约束）与问题3（固定稀疏度等式约束）。

从结构上看，前述的Model 2.1（即简化模型）虽已成功嵌入了逻辑稀疏判定机制，但其变量$z_i$的表达仍模糊——在$x_i=0$时，$z_i$可能取0，也可能取1。这种“软指示变量”的性质，使得模型更适合于处理不等式型约束（Problem 2），而对Problem 3中要求精确控制稀疏度的等式限制则显得力有未逮。因此，本文在Model 2.1的基础上提出两类增强方案，分别用于刻画问题2与问题3的QUBO实现。

4.1 不等式稀疏约束：将${\ell }_0$控制为上界

考虑目标函数为最小二乘项：

$$\underset{\mathbf{x},\mathbf{z}}{min}\parallel A\mathbf{x}-\mathbf{y}{\parallel }_2^2$$

辅以如下约束条件： (1)稀疏度控制为不超过$k$：

$$\sum _{i=1}^n{z}_i=k$$

(2)信号变量由二进制向量编码：

$$x_i=g({\delta }_i)$$$$\begin{gathered} z_i\ge {\delta }_{ij},j\in {\mathcal{I}}_0 \\ {z}_i\ge 1-{\delta }_{ij},j\in {\mathcal{I}}_1 \end{gathered}$$

这组约束确保了：只要$x_i\ne 0$，则$z_i=1$；反之若$x_i=0$，则$z_i$ 可以取0，即$z_i$的总和$\sum _i{z}_i$是$\parallel x{\parallel }_0$的上界。配合目标函数中的$\lambda \sum _i{z}_i$，该结构具有天然的稀疏性收缩效果，在不需要明确设置$\parallel x{\parallel }_0=k$的前提下即可控制稀疏度。

相比之下，HUBO（高阶无约束二进制优化）模型采用逐项幂展开（termwise quadratization），将形如$-\prod _i{b}_i$的负幂积项通过一个辅助变量$a$重写为：

$$-\prod _{i=1}^d{b}_i=\underset{a\in \{0,1\}}{min}\{(d-1)a-\sum _{i=1}^{d}a{b}_i\}$$

虽然这样能转化为QUBO，但存在两个缺陷：首先是变量维度显著扩张，需引入额外变量与高阶代价项； 其次是模型倾向于压缩$\parallel x{\parallel }_0$到极小，忽视约束条件中$k$的控制，从而更像${\ell }_0$正则问题而非${\ell }_0\le k$约束问题。

4.2 等式稀疏约束：精确控制$\parallel x{\parallel }_0=k$

为解决Problem 3所提出的精确稀疏度等式约束，本文进一步在Model 2.1基础上提出Model 2.2，通过更强约束直接令$z_i=0$当且仅当$x_i=0$，从而使$\sum _i{z}_i=\parallel x{\parallel }_0$成立，并可用于精确等式约束。具体约束形式为：

$$z_i\le \sum _{j\in {\mathcal{I}}_0}{\delta }_{ij}-\sum _{j\in {\mathcal{I}}_1}{\delta }_{ij}+|{\mathcal{I}}_1|,\mathrm{\forall }i\in [1,n]$$

解释如下：

• 当${\delta }_i={\delta }^{(0)}$，即$x_i=0$，则上式右端为$|{\mathcal{I}}_1|-|{\mathcal{I}}_1|=0$，强制$z_i\le 0$；
• 当$x_i\ne 0$，则右端$>0$，可允许$z_i=1$。 该条件保证了：若$x_i=0$，则$z_i=0$；反之则无强制要求。将此约束转化为QUBO表达形式，需要引入slack变量$s_i=\sum _j{2}^j\cdot s_{ij}$表示不等式右端余量，从而构造项：

$$\sum _{i=1}^n{(\sum _{j\in {\mathcal{I}}_0}{\delta }_{ij}-\sum _{j\in {\mathcal{I}}_1}{\delta }_{ij}+|{\mathcal{I}}_1|-z_i-s_i)}^2+{(\sum _{i=1}^n{z}_i-k)}^2$$

该项嵌入至原始QUBO表达式中，即可控制精确稀疏度$\parallel x{\parallel }_0=k$，从而模型2.2可有效求解Problem 3。

4.3 模型的扩展应用：量子支持向量机建模

本文提出的逻辑控制模型不仅适用于稀疏回归与压缩感知任务，也可自然扩展至稀疏分类问题中。进一步将该模型应用于${\ell }_0$正则支持向量机（SVM），其目标为：

$$\underset{\mathbf{w},b}{min}\lambda \parallel \mathbf{w}{\parallel }_0+\frac{1}{m}\sum _{i=1}^{m}max(0,1-y_i({\mathbf{w}}^{\mathrm{\top }}{\mathbf{x}}_i-b))$$

该问题通过引入辅助变量$r_i\in \{0,1\}$近似ReLU（Hinge）损失：

$$max(0,1-y_i({\mathbf{w}}^{\mathrm{\top }}{\mathbf{x}}_i-b))=r_i(1-y_i({\mathbf{w}}^{\mathrm{\top }}{\mathbf{x}}_i-b))$$

辅以以下约束：

$$M(r_i-1)\le 1-y_i({\mathbf{w}}^{\mathrm{\top }}{\mathbf{x}}_i-b)\le M{r}_i$$

其中$M$为足够大的常数。该结构能将SVM优化转化为QUBO表达，结合$\parallel \mathbf{w}{\parallel }_0$的二进制编码，构建出支持量子优化的稀疏分类器。

5. 固定表达下模型的理论保证

在本文提出的所有稀疏优化模型中，信号$x$均通过离散化编码方式表示，即每个信号变量由二值比特向量${\delta }_i\in \{0,1{\}}^K$所编码。由于这一量化过程本质上是一种有限字母映射，即将连续值信号投影到一个离散空间，所以在表达上不可避免地引入误差。我们将信号的量化过程形式化为：

$$Q:{\mathbb{R}}^n\to {\mathbb{R}}_Q^n,$$

其中${\mathbb{R}}_Q^n$表示所有量化后向量的值域集合。量化误差的最大失真量定义为：

$${ϵ}_Q=\underset{x\in {\mathbb{R}}^n}{sup}\parallel x-Q(x){\parallel }_2^2.$$

例如在模型使用的二进制编码情形下，若最大编码幅值为$\overline{x}$，比特数为$K$，则有：

$${ϵ}_Q=K\cdot {\overline{x}}^2\cdot 2^{-2K}.$$

为保证稀疏性结构在量化过程中不被破坏，我们假设$Q(\cdot )$为稀疏性保持型量化器，即：若$x_i=0$，则$Q(x{)}_i=0$；若$x_i\ne 0$，则$Q(x{)}_i\ne 0$。一个构造示例如下：

$$Q(x{)}_i=\{\begin{array}{ll}\lceil 2^K\cdot x_i\rceil /2^K,& x_i\ge 0\\ \lfloor 2^K\cdot x_i\rfloor /2^K,& x_i<0\end{array}.$$

在此设定下，若最优信号为$x^{\ast }$，而重构解为：

$$\hat{x}=\arg \underset{x\in {\mathbb{R}}_Q^n\cap S}{min}\parallel y-Ax{\parallel }_2^2,$$

其中$S$是满足某稀疏性限制的向量集合（如$\parallel x{\parallel }_0\le k$或$\parallel x{\parallel }_0=k$），则我们有以下结论。

定理 1： 对于Problem 2和Problem 3，或更一般的稀疏约束问题 (52)，若测量矩阵$A$满足RIP条件，定义其常数${\delta }_k(A)$为：

$$(1-{\delta }_k(A))\parallel v{\parallel }_2^2\le \parallel Av{\parallel }_2^2\le (1+{\delta }_k(A))\parallel v{\parallel }_2^2,\mathrm{\forall }v:\parallel v{\parallel }_0\le k,$$

则有以下误差界：

$$\parallel \hat{x}-x^{\ast }{\parallel }_2^2\le \frac{1+{\delta }_k(A)}{1-{\delta }_{2k}(A)}\cdot {ϵ}_Q.$$

证明要点： $Q(x^{\ast })$是可行解；由最优性有：

$$\parallel y-A\hat{x}{\parallel }_2^2\le \parallel y-AQ(x^{\ast }){\parallel }_2^2.$$

由于$y=A{x}^{\ast }$，左边有：

$$\parallel A(\hat{x}-x^{\ast }){\parallel }_2^2\ge (1-{\delta }_{2k}(A))\cdot \parallel \hat{x}-x^{\ast }{\parallel }_2^2;$$

右边有：

$$\parallel A(x^{\ast }-Q(x^{\ast })){\parallel }_2^2\le (1+{\delta }_k(A))\cdot {ϵ}_Q.$$

将上述不等式联立，即得结论，证毕。

定理 2： 设$\lambda \le \frac{(1-{\delta }_k(A))\cdot {ϵ}_Q}{k}$，则${\ell }_0$正则模型的解$\hat{x}$满足：

$$\parallel \hat{x}-x^{\ast }{\parallel }_2^2\le \frac{(3+{\delta }_k(A))\cdot {ϵ}_Q}{1-{\delta }_{2k}(A)}+{ϵ}_Q.$$

证明要点设目标函数为：

$$f(x)=\parallel Ax-y{\parallel }_2^2+\lambda \parallel x{\parallel }_0.$$

由于$Q(x^{\ast })$是可行解，且其${\ell }_0$项为$k$，故：

$$f(Q(x^{\ast }))\le (1+{\delta }_k(A))\cdot {ϵ}_Q+\lambda k\le 2{ϵ}_Q.$$

假设$\parallel Ax-y{\parallel }_2^2>2{ϵ}_Q$，则$f(\hat{x})>f(Q(x^{\ast }))$，与$\hat{x}$最优性矛盾。然后有：

$$\parallel \hat{x}-Q(x^{\ast }){\parallel }_2^2\le \frac{\parallel A(\hat{x}-Q(x^{\ast })){\parallel }_2^2}{1-{\delta }_{2k}(A)}\le \frac{(3+{\delta }_k(A))\cdot {ϵ}_Q}{1-{\delta }_{2k}(A)},$$

因此：

$$\parallel \hat{x}-x^{\ast }{\parallel }_2^2\le \parallel Q(x^{\ast })-x^{\ast }{\parallel }_2^2+\parallel \hat{x}-Q(x^{\ast }){\parallel }_2^2=\frac{(3+{\delta }_k(A))\cdot {ϵ}_Q}{1-{\delta }_{2k}(A)}+{ϵ}_Q.$$

证毕。

由以上两个定理可以推导出，本文提出的所有模型（无论是约束式还是正则式）在使用稀疏性保持的量化器$Q$后，其误差界均为$\mathcal{O}({ϵ}_Q)$。在使用$K$比特编码的情况下，${ϵ}_Q=\mathcal{O}(2^{-2K})$，因此：

$$K=\mathcal{O}(\log \frac{1}{\parallel x^{\ast }-\hat{x}{\parallel }_2^2}),$$

即达到一定精度所需的编码比特数具有对数增长关系。此外，本文指出，该误差界也适用于随机信号$x$的恢复问题，并进一步区分了两种不同的量化误差来源：

• 测量前观测噪声（observation noise）：$y=A(x+\text{nob})$；
• 测量后采样噪声（measurement noise）：$y=Ax+n$。 Reeves等人表明，观测噪声的影响通常小于测量噪声。理解这些噪声在压缩感知中的根本限制，将成为未来理论分析与量子硬件设计的重要方向。

6. 实验结果

本节基于第3.3节提出的Model 2.1展开实验验证，评估其在实际量子求解平台上的稀疏重构能力。本文共设计了四组实验，分别对应16、46、76与106个Ising自旋的QUBO规模。实验以合成信号与CIM设备结合，全面评估模型在不同稀疏度、不同比特精度下的性能表现。

6.1 数据生成过程

每组实验均从数据模拟开始，首先构造观测矩阵$A\in {\mathbb{R}}^{m\times n}$，其元素独立采样自$0,\pm 1$，服从伯努利分布。若$A$的每一列独立且等概率取值于$\{-1,0,+1\}$，则其满足RIP条件的概率在稀疏度线性增长的情况下仍然指数趋近于1，是压缩感知理论中常用的构造方式。

随后生成真实信号向量$x^{\ast }\in {\mathbb{R}}^n$，其稀疏度分别设为1, 2, 3, 4，对应每组实验中的真实稀疏解。每个非零分量赋值为1，即：

$$x_i^{\ast }=\{\begin{array}{ll}1,& i\in \text{支持集}\\ 0,& \text{否则}\end{array}$$

最后，通过$y=A{x}^{\ast }$得到观测向量$y$。该观测对$(A,y)$构成输入实例，通过构造对应的QUBO问题，并在CIM上执行解码重构操作。为可视化Ising结构随比特数扩展的变化，文章绘制了四个实例的耦合系数热力图（见图3）。

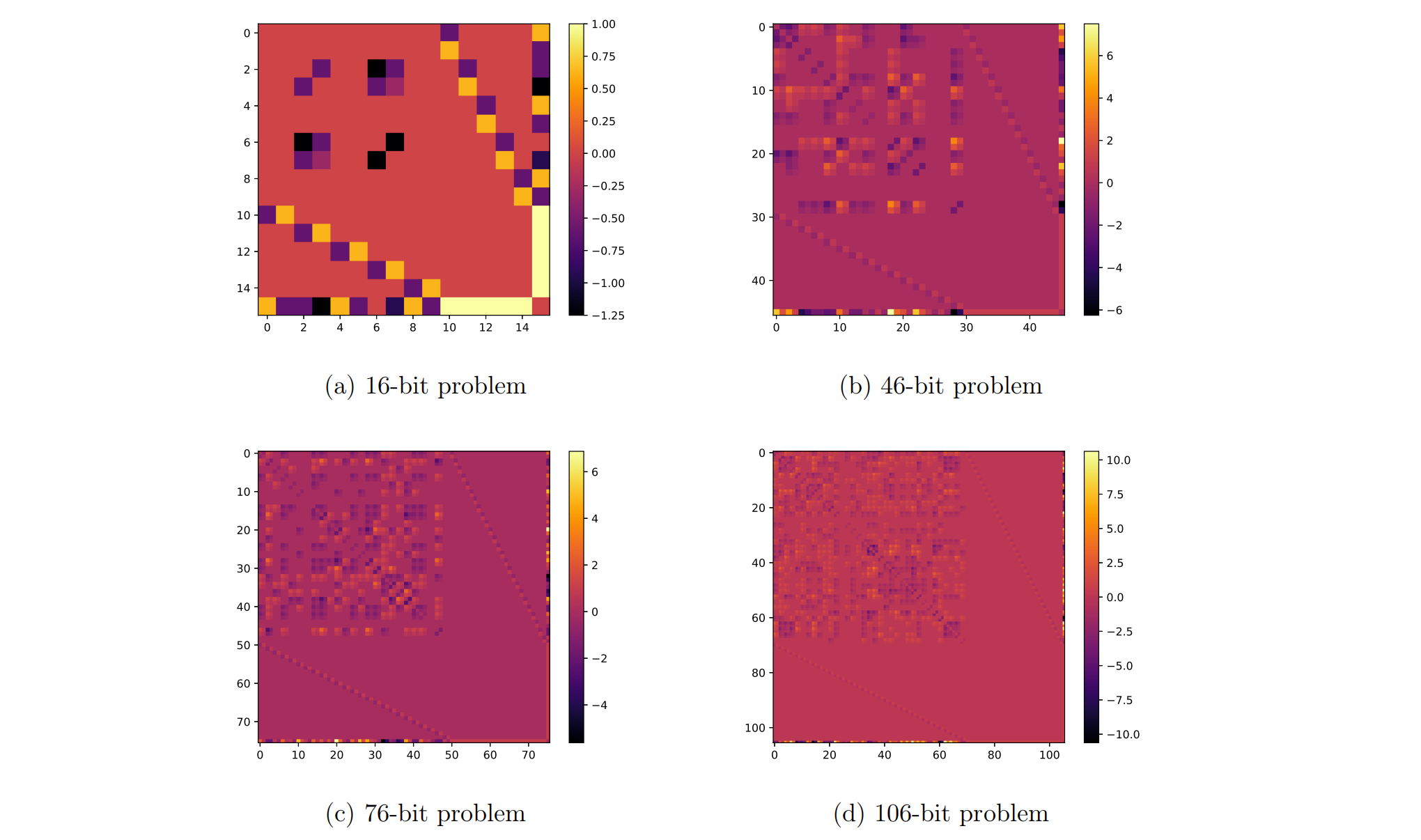
图3 四种问题对应的伊辛矩阵热力图。

每个热力图对应一个Ising系数矩阵（即QUBO经转换后的伊辛模型），图中颜色强度代表变量之间的耦合强度。随着比特数增加，图中结构由稀疏走向致密，展现出更复杂的变量交互模式与解空间几何。

6.2 方法说明

为全面评估CIM量子平台的求解性能，本文将其与五种经典算法进行了比较。对照方法包括三种压缩感知领域的代表性算法：正交匹配追踪（OMP）、去噪基础追踪（BPDN） 与LASSO；以及两种用于组合优化问题的经典启发式算法：模拟退火（SA） 与禁忌搜索（Tabu Search）：

• 模拟退火算法（Simulated Annealing, SA）：该方法模拟物理退火过程，以概率机制探索目标函数局部与全局最优解。在每一轮迭代中，算法考虑当前解邻域中的新解，并基于目标值差异与当前“温度”概率性地接受更差解，从而跳出局部最优陷阱。随着温度下降，算法趋于收敛，探索行为逐渐减少。
• 禁忌搜索算法（Tabu Search）：此方法是一种记忆驱动的组合优化策略。它维护一个“禁忌表”（Tabu List）以记录最近访问过的解或移动，防止循环与局部陷阱，并通过“愿望准则”（aspiration criteria）允许优解突破禁忌限制。此外，算法通过在解空间中强化或弱化特定路径，增强全局搜索能力。

在实验中，本文所使用的CIM平台为光学自旋模拟器，采用光纤环形腔中传输的脉冲作为模拟自旋的载体。其硬件结构如图4所示，包括：

• 1560nm飞秒锁模激光器（重复率100MHz）；
• 周期性极化铌酸锂（PPLN）非线性晶体；
• 光纤耦合器、平衡探测器（BHD）、模拟-数字转换器（AD）；
• 相位调制器（PM）、掺铒光纤放大器（EDFA）等关键部件。

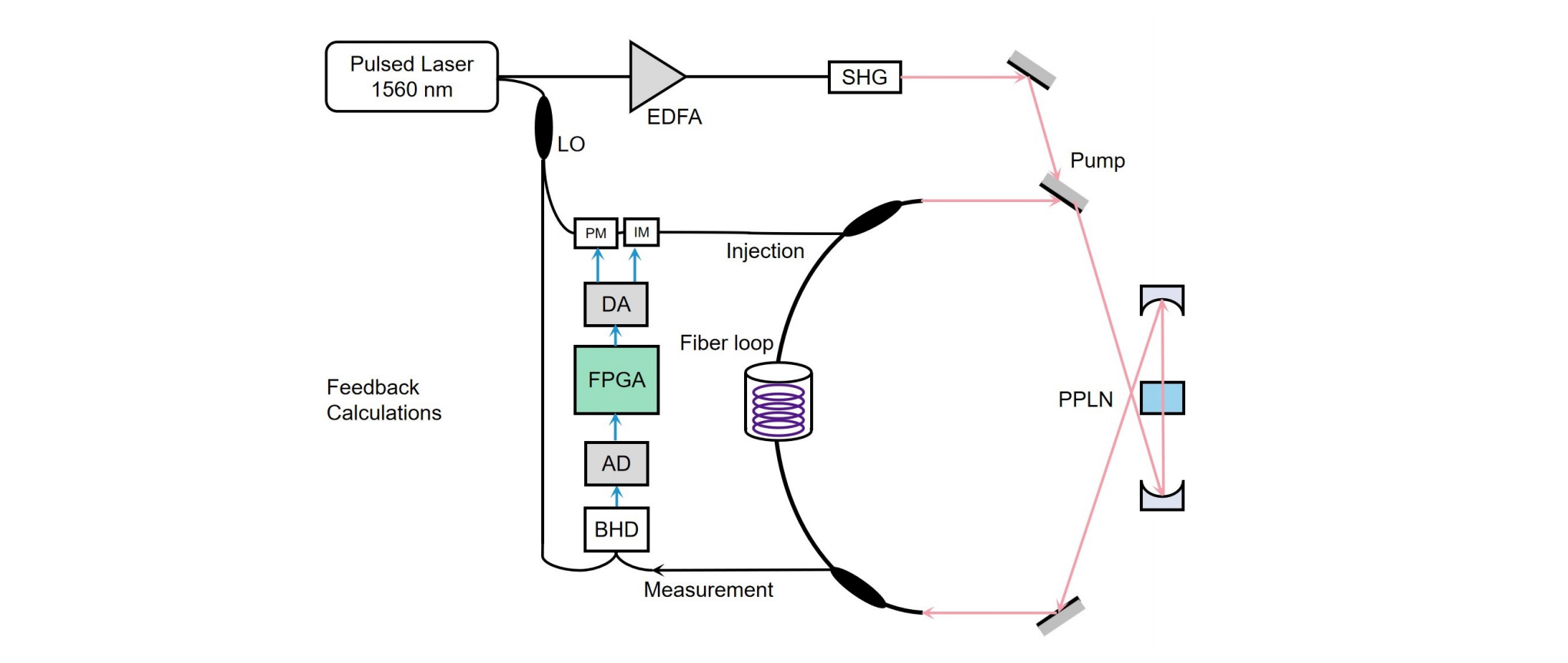
图4 相干伊辛机(CIM)系统示意图，展示了用于模拟量子动力学的集成系统及其关键组件，包括脉冲激光输入、掺铒光纤放大器(EDFA)、基于FPGA的反馈计算模块和测量单元

整个系统包含211个光脉冲，代表211个伊辛变量。所有测量数据经均衡探测后送入FPGA，由其根据耦合矩阵计算反馈信号，注入光腔以控制每轮脉冲演化，从而在物理意义上实现伊辛能量的动态最小化。为适配QUBO的非线性结构，本文采用一种标准方法将其转化为Max-Cut问题。在无磁场情形下，Ising模型的能量极小化问题可表示为：

$${\sigma }^{\ast }=\arg \underset{\sigma }{min}-\sum _{i,j}{J}_{ij}{\sigma }_i{\sigma }_j-\sum _i{h}_i{\sigma }_i$$

通过引入辅助自旋${\sigma }_a$，可以将线性项转化为双变量耦合项：

$$({\overline{\sigma }}^{\ast },{\sigma }_a^{\ast })=\arg \underset{\sigma ,{\sigma }_a}{min}-\sum _{i,j}{J}_{ij}{\sigma }_i{\sigma }_j-\sum _i{h}_i{\sigma }_i{\sigma }_a$$

最终恢复原问题解为${\sigma }^{\ast }={\overline{\sigma }}^{\ast }\cdot {\sigma }_a^{\ast }$。图5展示了76-bit Max-Cut问题的求解过程，节点以蓝色（$\sigma =+1$）与绿色（$\sigma =-1$）标记，图中边的分布表示解空间中变量间复杂的耦合关系。

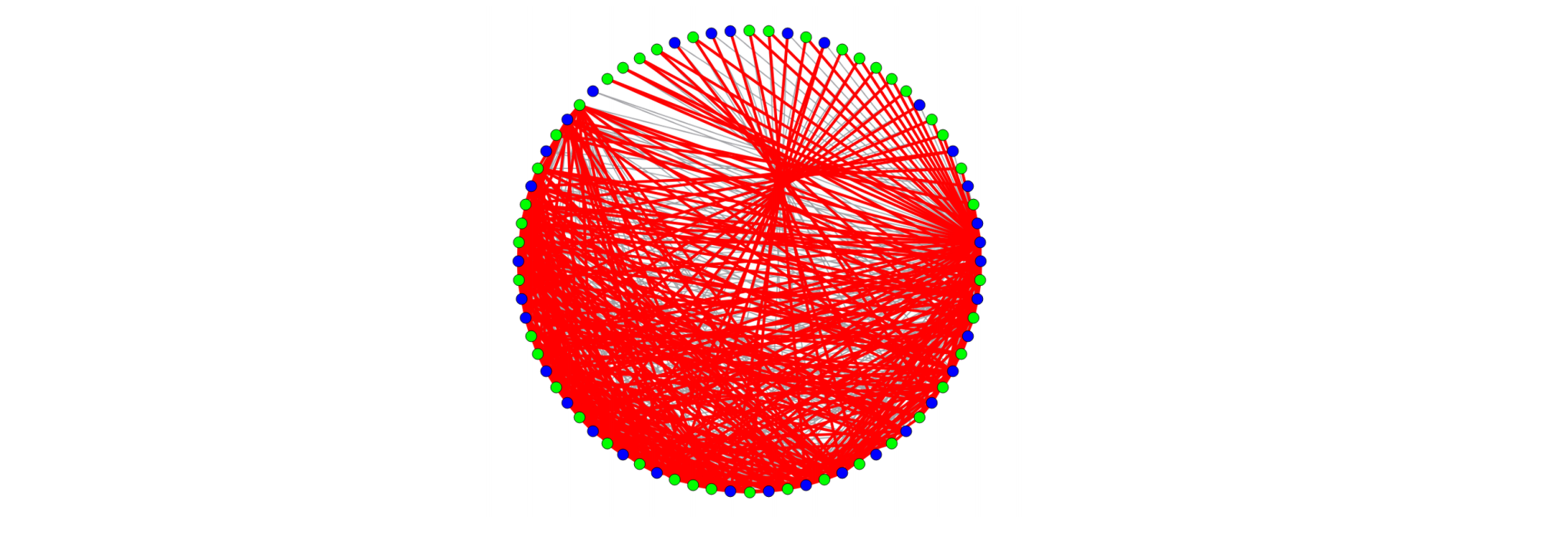
图5 76位最大割问题求解结果示意图。节点被划分为两类：一组节点以蓝色标识，代表自旋值为+1；另一组以绿色标识，代表自旋值为-1

6.3 实验结果分析

图6 展示了在不同问题规模下，CIM求解器在单次实验中Hamiltonian的演化轨迹。

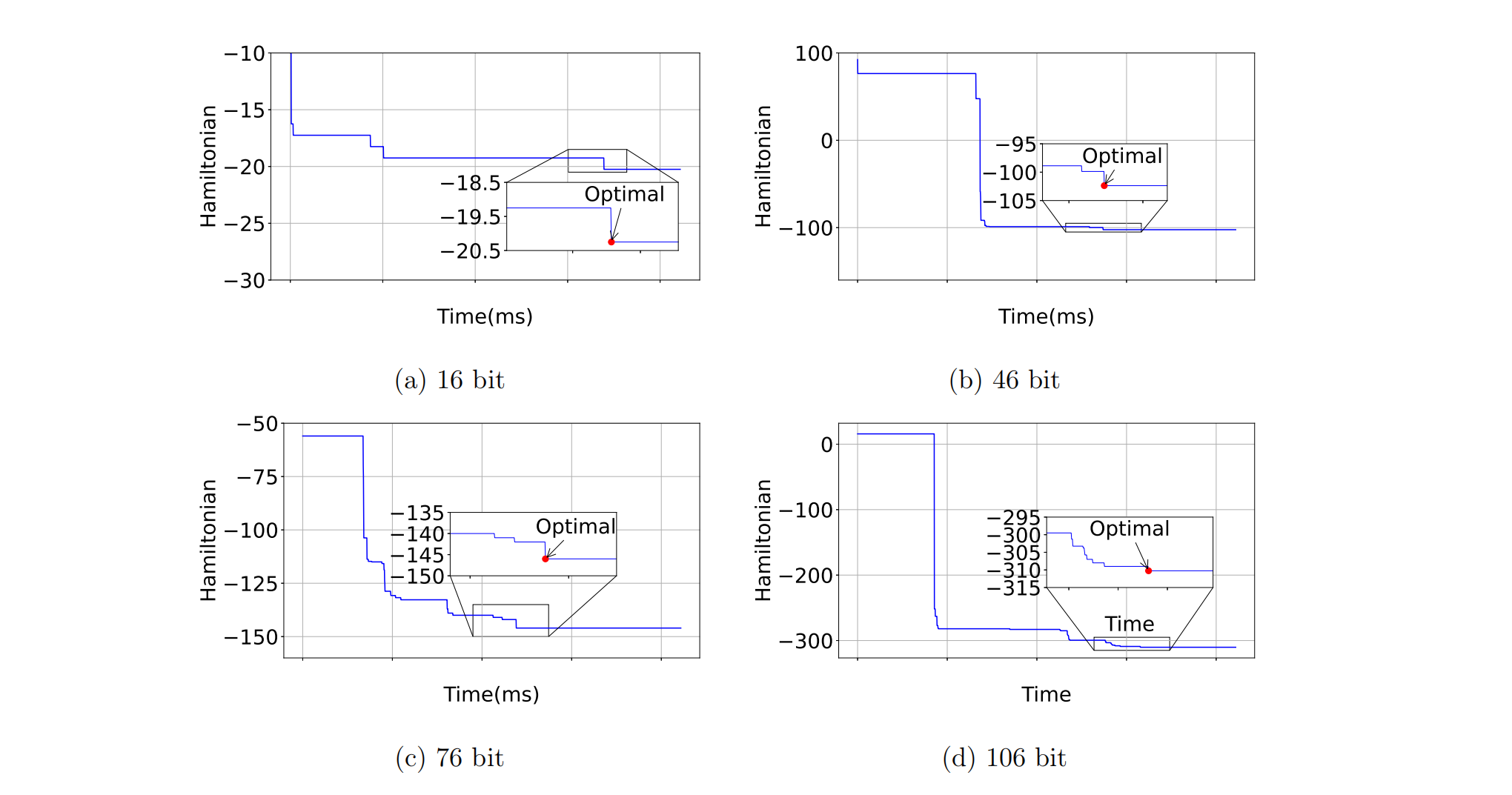
图6 不同系统规模下哈密顿量随时间演化的单次最优轨迹。主图区展示了四种不同比特长度系统（(a)16比特，(b)46比特，(c)76比特，(d)106比特）中哈密顿量（纵轴）随时间（横轴，毫秒单位）变化的动力学过程。红点标记最优能量态出现时刻，子图为特定关注区域的放大视图，详细呈现哈密顿量轨迹的波动特征

可以观察到，在极短的时间窗口内（不超过 3.39 毫秒），CIM能够迅速收敛至地面态，即目标函数最小值附近：

• 在16-bit问题中，Hamiltonian在3.25~3.5ms 区间收敛至$-20.5$；
• 在46-bit问题中，约于3.0ms时达到$-105$；
• 76-bit与106-bit问题中分别收敛至$-150$与$-315$附近；
• 每次相邻采样点的时间间隔为$2.11$微秒，源自光纤环形腔内$211$个光脉冲之间的$10$纳秒间距。 Hamiltonian的演化趋势为稳步下降，至泵浦功率达到临界值附近发生相变，系统进入稳定解态，表现出高度组织的能量收敛特性。图中嵌套的放大视图揭示了能量轨迹的微弱波动，反映了量子系统动态演化过程中的噪声与稳定性特征。

图7展示了不同问题规模下，CIM所得到的解在多次实验中的归一化均方误差（NMSE）与准确率的箱线图。

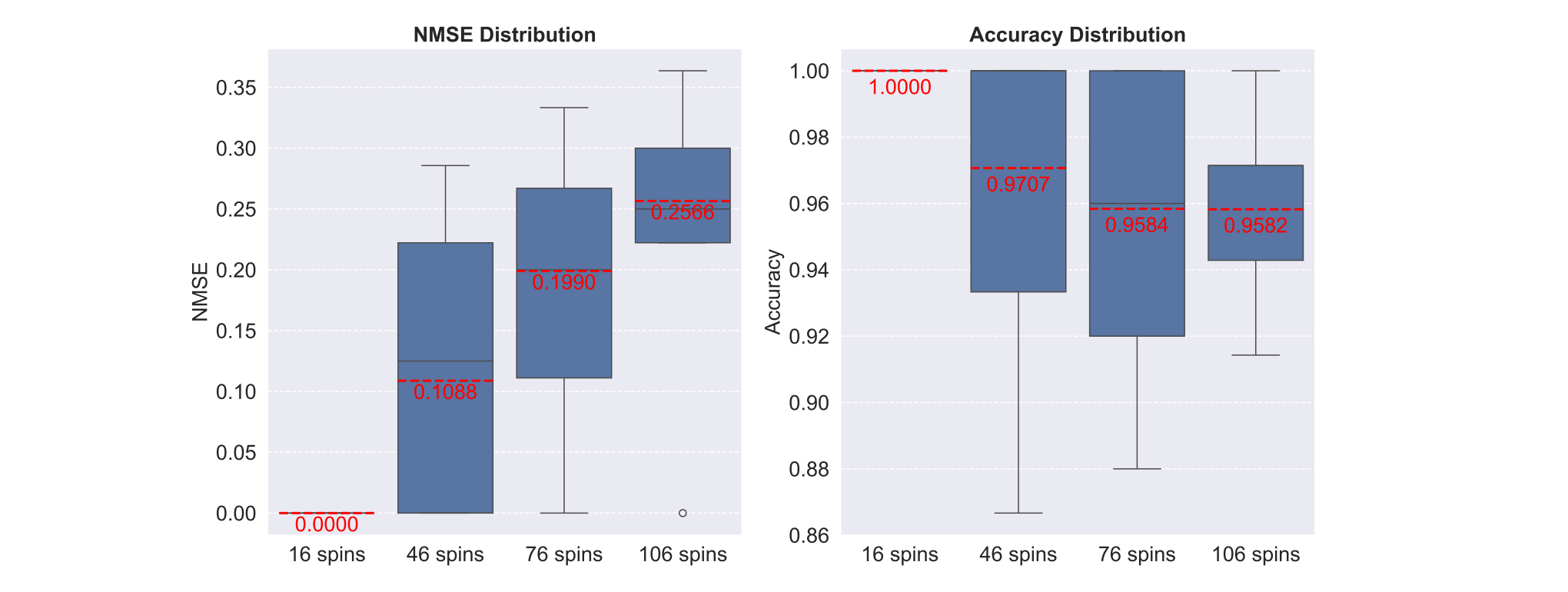
图7 相干伊辛机(CIM)在不同问题规模下的归一化均方误差(NMSE)与准确率箱线图分布，红色虚线标示各组数据的均值

结果显示，16-bit问题中CIM表现完美，NMSE为0，准确率达100%；随问题规模上升（46/76/106-bit），NMSE稍有上升，分别为$0.1088$、$0.1990$与$0.2566$，但准确率依然维持在$97.07\mathrm{\%}$、$95.84\mathrm{\%}$与$95.82\mathrm{\%}$附近。

此外，表2给出了多种方法在四组问题中的NMSE与准确率对比结果。CIM在所有问题规模下均实现了$0$的NMSE与$100\mathrm{\%}$的准确率，明显优于OMP、LASSO、BPDN及SA/Tabu两种运行时间设置下的表现。定义NMSE为：

$$\text{NMSE}=\frac{\parallel x_{\text{true}}-x{\parallel }_2^2}{\parallel x{\parallel }_2^2},$$

准确率定义为：

$$\text{Accuracy}=\frac{|\{i|x_i^{\ast }=0,x_i=0\}|+|\{i|x_i^{\ast }\ne 0,x_i\ne 0\}|}{n}.$$

实验设置	算法	NMSE	Accuracy	实验设置	算法	NMSE	Accuracy
m = 2, n = 5, k = 1	OMP	0.0000	100.00%	m = 5, n = 25, k = 3	OMP	0.0000	100.00%
	LASSO	0.0008	100.00%		LASSO	1.1137	84.00%
	BPDN	0.0064	80.00%		BPDN	0.0043	88.00%
	SAshort	0.3320	80.00%		SAshort	1.0475	50.08%
	SAlong	0.1700	87.20%		SAlong	1.0726	74.72%
	Tabushort	0.5879	75.60%		Tabushort	1.0858	60.64%
	Tabulong	0.2930	76.80%		Tabulong	0.9912	61.44%
	CIM	0.0000	100.00%		CIM	0.0000	100.00%
m = 5, n = 15, k = 2	OMP	1.6000	86.67%	m = 7, n = 35, k = 4	OMP	0.2737	94.29%
	LASSO	1.3525	86.67%		LASSO	0.7348	94.29%
	BPDN	0.4009	33.33%		BPDN	0.2705	14.29%
	SAshort	0.8630	60.40%		SAshort	1.0111	44.80%
	SAlong	0.4109	90.53%		SAlong	0.9856	68.51%
	Tabushort	0.8958	65.73%		Tabushort	1.0100	59.20%
	Tabulong	0.8184	68.53%		Tabulong	0.9858	58.06%
	CIM	0.0000	100.00%		CIM	0.0000	100.00%

表2 相干伊辛机(CIM)与经典算法的性能对比。针对模拟退火(SA)和禁忌搜索(Tabu)算法，我们测试了两种不同运行时长：SA的短时运行版本(SAshort)平均耗时约0.16秒（四次实验具体耗时分别为0.1531秒、0.1570秒、0.1616秒、0.1611秒）；其长时运行版本(SAlong)平均耗时约15秒（具体耗时14.96秒、15.09秒、15.78秒、15.72秒）。Tabu的短时版本(Tabushort)平均耗时约0.1秒（0.0756秒、0.0813秒、0.0917秒、0.1276秒），长时版本(Tabulong)平均耗时约0.8秒（0.5717秒、0.7129秒、0.8149秒、1.0518秒）。实验数据表明，增加运行时间可有效提升SA与Tabu两类算法的求解性能。

图8对比了不同方法在达到目标精度下的“目标时间”（Time To Target, TTT）。该指标衡量随机算法在达到指定成功概率$p_0$（此处为 $0.99$）下所需的平均时间，定义为：

$$\text{TTT}=\tau \cdot \frac{\log (1-p_0)}{\log (1-p_{\tau })},$$

其中$\tau$是单次运行时间，$p_{\tau }$是单次命中目标解的概率。

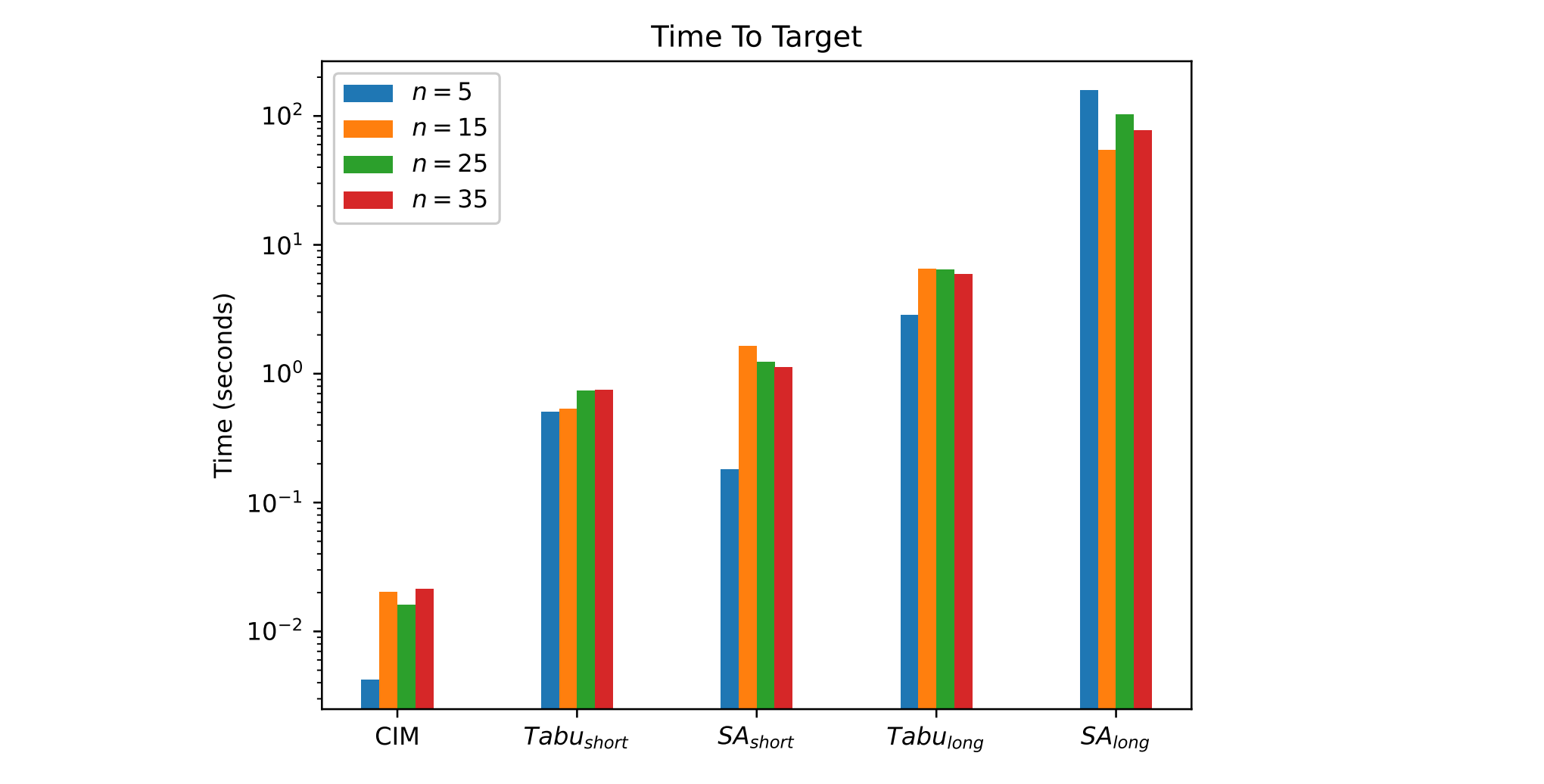
图8 多种方法的达标时间(TTT)对比。相干伊辛机(CIM)、禁忌搜索(Tabu)和模拟退火(SA)三种方法在不同问题规模下的性能表现通过颜色区分：蓝色(n=5)、橙色(n=15)、绿色(n=25)和红色(n=35)

CIM的$\tau =2000\times 2.11\mu s=4.22ms$，SA与Tabu的$\tau$则为各自运行中超过目标精度所需的最长时间。图中蓝、橙、绿、红分别表示变量规模为$n=5,15,25,35$。结果显示：尽管SA与Tabu在长时间运行下可提升精度，但CIM在TTT指标上依然显著优越，说明其不仅准确，而且收敛速度快。

6.4 混合算法性能评估

在本实验中，本文进一步对比了两种QUBO求解策略的复杂度：

• 直接QUBO编码（Direct QUBO modeling）：将所有变量（包括幅度编码、稀疏指示等）直接表示为$n(K+1)$个二进制变量；
• Benders分解策略（Quantum Benders decomposition）：将结构变量$z$留给量子模块求解，连续变量$x$交由经典模块处理。

实验表明，Benders方法在每次迭代中显式维护上下界，通过不断逼近目标函数值，有效地缩小了解空间。图中灰色区域表示上下界间的误差带，随迭代次数递减，反映出算法的稳定收敛特性。

此外，Benders分解后的主问题（RMP）只涉及$2n$个二值变量和一个连续变量，且约束数量等于迭代次数。相比于直接QUBO表达，其量子模块所需的qubit数大幅减少，特别适用于当前量子硬件所支持的比特规模限制。在RMP的优化中，本文进一步建议结合 Quantum Conditional Gradient Method，以更高效地处理受限优化结构，进一步提高量子-经典协同算法的实用性与可扩展性。

7. 讨论与总结

尽管本文展示了基于CIM平台的稀疏优化方法在建模能力与求解效率方面的显著优势，但必须指出，硬件层面的现实制约仍对算法性能存在一定影响。其中最根本的限制在于参数精度——虽然QUBO框架理论上允许连续实值参数，但实际物理设备中的数值表示始终受限于有限位宽与模拟精度，导致所映射的系数矩阵存在近似误差，从而可能影响最终解的准确性。图9展示了在Benders分解方法下，不同问题规模中上下界的收敛情况。

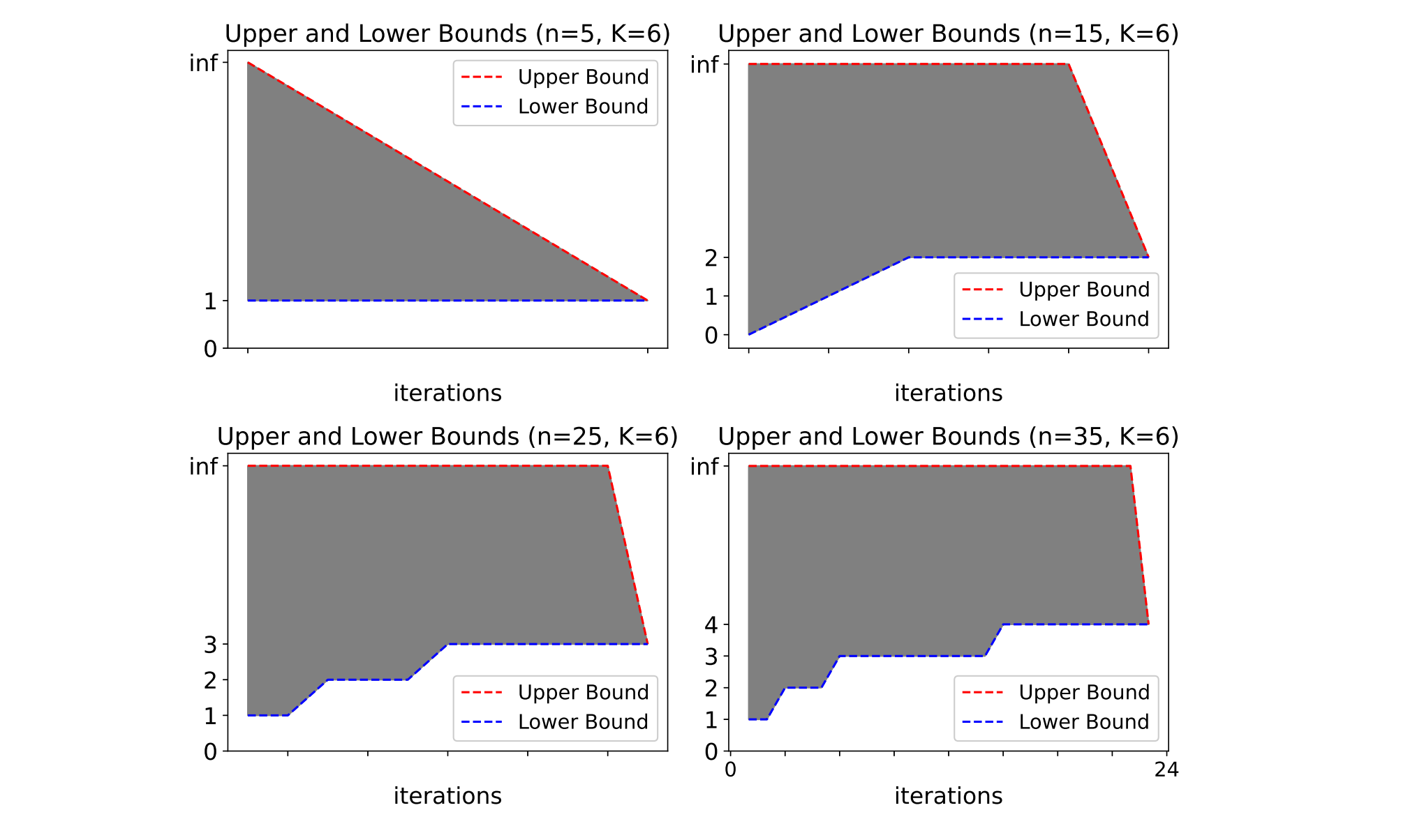
图9 稀疏优化问题中Benders分解法的上下界收敛过程。子图分别对应信号长度n=5、15、25和35的情况，其中K=6表示每个实数变量编码为二进制变量时所需的伊辛自旋数

可以看出，随着迭代次数增加，解空间被逐步压缩，上下界之间的差距持续收敛。这一现象不仅验证了混合算法的稳定性，也间接揭示了有限比特表示下系统在收敛过程中的表现边界。

尽管存在精度限制，近年来有关CIM的理论研究已逐步深入，为其求解机制提供了更坚实的数学基础。尽管文中所用CIM实现与OEO-CIM并不完全一致，但OEO-CIM的理论框架为理解广义CIM系统的优化能力提供了重要参考。

基于上述模型建构、量子映射、混合算法与实证实验，本文完成了从稀疏建模理论到物理实现机制的全面打通，所提出的工作不仅验证了量子近似硬件（如CIM）在求解NP-hard稀疏优化问题中的潜力，也为经典方法与量子技术的融合探索出可行路径。

本文的贡献主要体现在以下三个方面：

1. 统一建模框架：通过构建多种稀疏优化问题（正则项、约束式与固定稀疏度）的一体化QUBO表达，实现了${\ell }_0$-优化问题在量子求解器上的通用编码。
2. 混合解法机制：提出基于Benders分解的量子-经典协同策略，显著降低了变量规模，提高了解空间收敛速度，为硬件适配性提供了工程可行性。
3. 实证性能验证：在多个规模下，通过实验对比OMP、LASSO、BPDN、SA与Tabu等方法，CIM在准确率、误差表现与运行时间方面均显著领先，特别是在低时间预算下具备更优的TTT（Time-To-Target）表现。

总体而言，本文展示了稀疏性原理与量子优化硬件融合的巨大潜力——稀疏性与量子计算的结合，不仅是一种算法技术的更新，更可能是信息处理范式的革新。在未来的研究中，一方面可以进一步探索不同量子架构（如gate-based quantum processor）下的QUBO表达能力；另一方面，也有望结合实际高维稀疏应用（如图像重建、神经网络剪枝与图信号处理）进行推广，推动量子优化模型的跨学科落地。

论文链接：量子架构与混合技术驱动的统一稀疏优化方法