基于量子计算的云柜台柜员调度技术问题

摘要：随着金融行业数字化转型的不断推进，银行云柜台柜员调度问题成为了一个亟待解决的挑战。传统的调度方法依赖于统计分析，存在计算效率低、容易陷入局部最优解等问题。

为了解决这些问题，本文提出了一种基于量子计算算法的银行云柜台柜员调度方案。该方案利用排队论对客户到达和服务时间进行建模，并将调度问题转化为二次无约束二元值优化（QUBO）模型，通过光量子相干伊辛机进行求解。实验结果表明，该方案在计算速度和求解质量上均显著优于传统算法，能够在极短时间内找到全局最优解，有效降低金融服务成本，提高服务效率。本文的研究不仅为银行云柜台柜员调度问题提供了一种新的解决方案，也为量子计算在运筹学中的应用提供了有益的探索。

关键词：量子计算；云柜台柜员调度；排队论；QUBO模型；光量子相干伊辛机

1. 背景介绍

中国邮政储蓄可追溯至1919年开办的邮政储金业务，至今已有百年历史。至今已拥有近4万个营业网点，服务个人客户超6.6亿户，为聚焦降本增效，着力推动集约化转型，云柜台正在成为重要面客端口，通过不断创新技术手段，与数字人、语音识别、语义理解等AI技术深度融合，优化业务办理流程，实现云柜业务智能导航、自动授权、主动营销等创新能力，达到降低集约化运营成本，提高云柜服务效率的目标。

云柜台的智能化势在必行，但仍无法完全脱离人工服务，尤其是高风险、高复杂度、个性化交易的业务仅能由人工处理。为在峰时持续提供优质服务，云柜中心需要将合理时间配置合理数量的柜员，因此柜员调度是该场景需要解决的规划问题。

目前的解决方案是利用统计方法总结前周每天的业务量占比，并基于该比例预测接下来一段时间需要安排的柜员人数。该种方法较为便捷但忽略了季节性影响，并且为保证客户体验，更多时间以冗余形式运行，忽略了更加精细化的成本控制。在银行业数字化转型及降本增效的大趋势下，该场景存在技术创新的空间。

2. 问题描述

调度是规划求解问题的一类，规划求解又是金融领域中较为常见的复杂数学问题，规划求解问题往往需要消耗大量计算资源。量子计算作为一种前沿科技手段，可以有效处理此类问题，并以较低的计算资源快速得到规划最优解。

本方案可以为同业绿色金融转型提供案例参考，借用量子计算高效的计算能力，在保证金融服务质量稳定高效前提下，金融机构可以在算力侧及人工侧降低金融服务成本，既推动金融的普惠性，又完成金融机构降本增效，推动数智化转型的阶段任务。

柜员调度问题是规划求解问题中较为典型的一类，与投资组合优化、套利路径寻优等均为同源性问题。此类问题的计算复杂度会随着变量增多以指数级增长。经典算法在处理此类问题时，所需要的计算时间和计算资源会随问题复杂度的提高以指数级增长，同时在特定时间内找到最优解也存在一定的局限性，容易陷入局部最优解。因此，本方案借助该场景对量子计算技术进行探索，通过尝试量子算法，为此类规划问题提供新的解决方案。

QUBO数学建模是通过引入二元值变量，将规划问题中的损失函数转化为二元值整数规划问题。通过此类转换可以将传统规划问题转化为光量子相干伊辛机易于处理的Ising模型，从而能够利用量子计算机的强大计算能力。

3. 算法实现过程

本方案由三个部分构成：第一部分是统计分析工具，通过对大量历史数据进行统计得到每天各个时间窗口接待客户占当天业务量的比例的估计值，经统计推断证明该比例维持一个稳定的分布，同时对顾客到达间隔时间以及柜员服务时间进行统计判断，获得相应分布。在本例中，顾客以泊松（Poisson）分布接入云柜台，柜员服务时间服从爱尔朗（Erlang）分布。

第二部分为数据建模，顾客接入云柜台前先进入单队列再分配至不同柜台，在排队论中是一个典型的单队列多柜台问题，可以使用M/G/n模型对该流程进行表示，得到该模型下顾客平均等待时间T与柜员人数n之间的数学关系，如下：

$$t_{\mathrm{i}}=[\frac{1+v^2}{2}+(1-v^2)(1-{\rho }_{\mathrm{i}})(n_{\mathrm{i}}-1)\frac{\sqrt{4+5n_{\mathrm{i}}}-2}{16{\rho }_{\mathrm{i}}{n}_{\mathrm{i}}}]\cdot t_1^{M/M/n_1}$$

基于该数学公式可以构建以n为变量的映射函数，将问题转化到整数规划方向。

第三部分为规划求解。本场景下共有21个时间窗口,共有柜员60人，因此解空间有60的21次方之多。方案将损失函数转化为二次无约束二元值优化（QUBO）模型再转化到光量子相干伊辛机（CIM）可以计算的Ising模型，然后使用光量子相干伊辛机进行求解。要构建QUBO模型，可以首先使用以上排队论公式对每一个可能的柜员数所对应的顾客平均等待时间都进行计算，以表格的形式呈现从柜员数到顾客平均等待时间的映射关系。然后将优化问题转换为在每一个时间窗口分配一个合理的柜员人数，即表格的每一行选一列的二元值整数规划问题。由此决策变量为$21\times 60$的二进制矩阵$x_{ij}$，其中$x_{ij}=1$代表第$i$个时间窗口分配$j$位柜员。

由此，可得最小化柜员总工时的目标函数1：

$$min\sum _{i=1}^{21}\sum _{j=1}^{60}{n}_{ij}{x}_{ij}$$

和最小化各个时间窗口客户平均等待时间的最大值的目标函数2：

$$minu$$$$\sum _{j=1}^{60}{t}_{ij}{x}_{ij}-u\le 0，\mathrm{\forall }i\in \{1,2,\dots ,21\}$$

以及一系列根据每日工时、云柜中心最大人数限制等引出的约束条件。

4. 结论

1. 使用光量子相干伊辛机完成对柜员调度这类整数规划问题的求解和实际应用，验证量子计算机在真实场景的实用性，为大规模组合优化方法创造了先决的条件；

2. 图1展示了实际柜员数和量子算法计算出的理论最优值的对比，可以看到在队列不增长且客户等待满足业务要求情况下，量子算法给出了柜员人数的理论下限，为云柜中心提供了每个时间窗口需安排最低柜员人数的数学参考。其次，本次计算是在60的21次方解空间中寻优，光量子相干伊辛机的计算时间为4.8±0.4ms，使用商用求解器Gurobi求解该数量级解空间为105±5ms（Intel 13代 Core i5-13600K 14核20线程并行计算），相较于传统算法光量子相干伊辛机在计算速度上提高了20余倍。

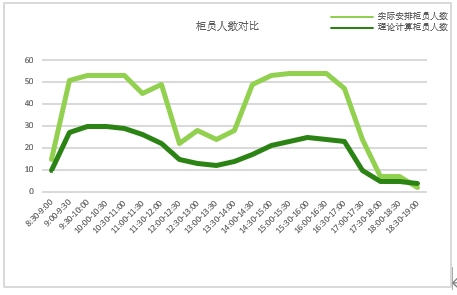图1：柜员人员对比

5. 场景延展

本案例是业内首次将基于光量子相干伊辛机的量子计算技术应用于银行云柜台柜员调度优化场景，是应用量子计算机求解NP难的整数规划问题的一个创新案例。引入光量子相干伊辛机开辟了量子计算与运筹学领域融合的新应用路径，以下场景是涉及到运筹学调度的应用：

1. 算力规划：在满足服务器约束的同时，使用尽可能少的服务器数量完成计算任务，并协助云计算服务提供商找到调度计算资源的最佳方案；

2. 地铁规划：基于乘客的动态变化和时空分布不平衡，寻找符合的地铁灵活编组策略；

3. 电力规划：基于发电量、用电量、电价等数据信息制定更加经济、合理的电力分配方案，实现削峰填谷的电网稳定优化方案。