3.4 新手教程

最大割问题

最大割问题是NP完备问题。给定一张图，求一种分割方法将所有顶点分割成两部分，同时使得被切断的边的数量最大或边的总权重最大。

以无向无权图为例，在图 $G(V,E)$中，$V$为图的顶点集合，$E$为图的边集，$w$为图的邻接矩阵。对于$i,j\in V$，$w_{ij}$表示顶点$i$到顶点$j$是否有边，有连边关系则取$1$，无连边关系则取$0$。以决策变量$s_i$表示顶点$i$的分类，其可能的取值为 $1,-1$，分别表示将顶点$i$分为A类或B类。

则在给定的无向图中，将所有顶点分割成两群的分割方法所对应割的边的个数为Z，模型表示为：

$$maxZ=\frac{1}{2}(\sum _{\begin{array}{c}i<j\\ i\in V\end{array}}\sum _{j\in V}{w}_{ij}-\sum _{\begin{array}{c}i<j\\ i\in V\end{array}}\sum _{j\in V}{w}_{ij}{s}_i{s}_j)$$

以一个四顶点实例说明，如下图所示，通过观察可以发现将1、2分为A类，3、4分为B类的“割”法将得到问题的最优解$Z=4$。

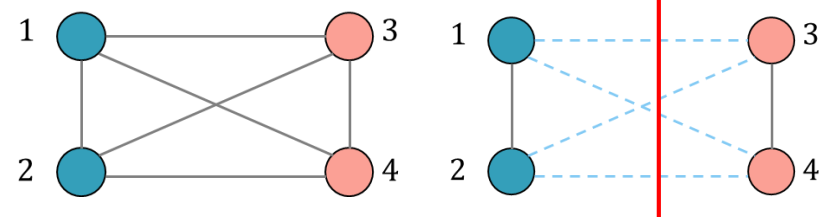
通过连边关系可知，邻接矩阵为：

$$\sum _{i<j,i\in V}\sum _{j\in V}{w}_{ij}=w_{12}+w_{13}+w_{14}+w_{23}+w_{24}+w_{34}$$$$\sum _{i<j,i\in V}\sum _{j\in V}{w}_{ij}{s}_i{s}_j=w_{12}{s}_1{s}_2+w_{13}{s}_1{s}_3+w_{14}{s}_1{s}_4+w_{23}{s}_2{s}_3+w_{24}{s}_2{s}_4+w_{34}{s}_3{s}_4$$

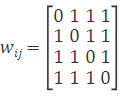
当顶点1、2为一组，顶点3、4为另一组时，$s_1=s_2=1,s_3=s_4=-1$.则上式变为：

$$\sum _{i<j,i\in V}\sum _{j\in V}{w}_{ij}{s}_i{s}_j=w_{12}-w_{13}-w_{14}-w_{23}-w_{24}+w_{34}$$

此时目标函数为：

$$maxZ=\frac{\sum _{i<j,i\in V}\sum _{j\in V}{w}_{ij}-\sum _{i<j,i\in V}\sum _{j\in V}{w}_{ij}{s}_i{s}_j}{2}=w_{13}+w_{14}+w_{23}+w_{24}=4$$

最大割数量为4，符合前文通过观察得到的答案。

注意到，$w_{ij}$为输入的常量，并不影响模型的计算，所以上式可以简化为：

$$minH=\sum _{i<j,i\in V}\sum _{j\in V}{w}_{ij}{s}_i{s}_j$$

其中, $H$表示哈密尔顿量，$w$为输入的邻接矩阵，决策变量$s_i$表示顶点$i$的分类，上述式子就是一个最大割问题的Ising模型。

建模代码

输入矩阵

矩阵表示N个节点的连接关系，如果两个点之间有边，就用1表示，没有边，就用0表示。

import numpy as np
import kaiwu as kw

# Import the plotting library
import matplotlib.pyplot as plt

# invert input graph matrix
matrix = -np.array([
                [0, 1, 0, 1, 1, 0, 0, 1, 1, 0],
                [1, 0, 1, 0, 0, 1, 1, 1, 0, 0],
                [0, 1, 0, 1, 1, 0, 0, 0, 1, 0],
                [1, 0, 1, 0, 0, 1, 1, 0 ,1, 0],
                [1, 0, 1, 0, 0, 1, 0, 1, 0, 1],
                [0, 1, 0, 1, 1, 0, 0, 0, 1, 1],
                [0, 1, 0, 1, 0, 0, 0, 0, 0, 1],
                [1, 1, 0, 0, 1, 0, 0, 0, 1, 0],
                [1, 0, 1, 1, 0, 1, 0, 1, 0, 1],
                [0, 0, 0, 0, 1, 1, 1, 0, 1, 0]])

使用经典求解器进行计算

由于Maxcut问题矩阵就是一个Ising矩阵，所以可以调用SDK提供Optimizer直接求解，本例中使用SimulatedAnnealingOptimizer。

worker = kw.classical.SimulatedAnnealingOptimizer(initial_temperature=100,
                                                  alpha=0.99,
                                                  cutoff_temperature=0.001,
                                                  iterations_per_t=10,
                                                  size_limit=100)
output = worker.solve(matrix)

输出结果

从输出的多个解中拿到最好的那个解，通过最好解和原来的矩阵算出最大割的值并输出。

opt = kw.sampler.optimal_sampler(matrix, output, 0)
best = opt[0][0]
max_cut = (np.sum(-matrix)-np.dot(-matrix,best).dot(best))/4
print("The obtained max cut is " + str(max_cut) + ".")