案例解析：量子计算优化高价值支付系统流动性效率研究

1. 研究背景

银行支付系统每日需要结算大量的交易，需要在结算账户里预留足够的现金，而这部分现金因为无法用来投资或放贷，故属于银行的机会成本（丧失了用钱生钱的机会）。因此最小化银行的机会成本（行业专有名称是“流动性成本”）是我们优化的第一个目标。

一个很符合常理的优化方式是调整支付的结算顺序，使得多数支付能够被之前的入账所抵消（即使用入账现金支付），从而减少对预留现金的依赖。但是重新排序支付结算顺序必然导致支付的延迟，因此最小化排序后的平均支付延迟是我们优化的第二个目标。

重新排序支付会导致一个NP-hard的组合优化问题，其规模随着未结支付数量的增加呈指数级增长$O(n!)$，但也因如此专用量子计算机可以发挥其在求解组合优化问题速度上的优势。

2. 优化流程

假设首先设定一个固定大小$n$的支付批量大小（batch size），一旦收到的支付请求数量达到这个大小，优化过程就会被触发。

每一个批次的排序优化由专用量子计算机（D-wave量子退火机）+经典计算机实现。首先使用量子计算机多次求解，然后用经典计算机在可行解里挑选最好的解。所有支付请求按批次优化，不预测未来可能收到的支付请求。

2.1 优化目标定义

每个支付请求按$i=1,\dots ,n$索引。为了衡量系统所需要的流动性，我们首先定义$N(i)$为参与者在支付$i$被结算之前的净头寸。参与者的净头寸是其流动性余额，考虑了当天截至当前时刻所有进出支付的情况。

定义NDP（Net Debit Position）为某个交易参与者的净借方头寸。如果某个参与者的净借方头寸为正，则意味着对该参与者的支付义务（即待结算的支付）超过了其账户中的可用流动性。换句话说，他们在某一时刻需要更多的资金来完成支付。

定义mNDP（max NDP）为交易参与者在当天任何时刻经历的最大净借方头寸。如果一个参与者在一天开始时的$N=0$，那么在所有支付结算后的mNDP就衡量了为完成对该参与者的支付义务所需的最小现金额。因此，我们可以将mNDP看作该参与者的最小流动性需求，通过减少所有参与者的mNDP总和，在保持支付金额和结算延迟不变的情况下，代表了系统流动性效率的提升。

2.2 量子计算机的优化作用

量子计算机通过替代索引按$t=1,\dots ,n$重新排列支付请求队列，以实现最小化总流动性需求的目标，同时满足以下约束条件：

（1）任何参与者在任何时刻都不会进入负流动性状态，即始终有足够的现金满足该参与者的下一个支付请求；

（2）且所有支付都必须被处理，不得滞留在队列中。

3. 建模

定义二元值决策变量$x_{i,t}$为支付请求$i$是否在最终队列里的位置$t$处被结算：

• 若$x_{i,t}=1$则支付请求$i$在队列里的位置$t$处被结算；

• 若$x_{i,t}=0$则支付请求$i$未在队列里的位置$t$ 处被结算。

由该二元值决策变量的定义可知我们有以下两个约束条件：

• 支付请求$i$被且只被结算一次：$\sum _t{x}_{i,t}=1$
• 在队列位置$t$有且仅有一个支付请求被结算一次：$\sum _i{x}_{i,t}=1$

使用上二元值决策变量，我们可以表示参与者$\alpha$在任何时刻都不会进入负流动性状态的约束条件：

$$b_{\alpha }+N_{\alpha }(0)+mND{P}_{\alpha }+\sum _i\sum _{\tau \le t}f(\alpha ,i)x_{i,\tau }\ge 0\mathrm{\forall }\alpha$$

其中$b_{\alpha }$是分配给参与者$\alpha$的现金，当该值最小化时，它表示为了结算该批次的参与者$\alpha$的请求支付所需要的额外流动性现金。等效地，它也表示在该批次支付结算后参与者$\alpha$的最大净借方头寸$mND{P}_{\alpha }$的增加量。

而$f(\alpha ,i)$是一个函数，当$\alpha$是收款方时返回$v$（支付请求$i$的金额）；而当$\alpha$是付款方时返回$-v$，否则返回0。

本优化问题的优化目标是最小化银行的流动性成本，即分配给所有参与者的现金：

$$min\sum _{\alpha }{b}_{\alpha }$$

为了形成该优化问题的QUBO模型，我们引入了松弛变量$s_{\alpha }(t)$和惩罚系数${\lambda }_1$来表示以上不会进入负流动性状态的不等式约束条件。同样地，使用相同的惩罚系数${\lambda }_2$来表示关于二元值决策变量的两个等式约束条件。

使用上述二元值决策变量和约束表达方式，可得到如下QUBO模型：

$$\begin{array}{rl}H=& \sum _{\alpha }{b}_{\alpha }+{\lambda }_1\sum _{\alpha ,t}{(b_{\alpha }+N_{\alpha }(0)+mND{P}_{\alpha }+\sum _i\sum _{\tau \le t}f(\alpha ,i)x_{i,\tau }-s_{\alpha }(t))}^2\\ & +{\lambda }_2\sum _i{(1-\sum _t{x}_{i,t})}^2+{\lambda }_2\sum _t{(1-\sum _i{x}_{i,t})}^2\end{array}$$

在变量集$\{b_{\alpha },x_{i,t},s_{\alpha }(t)\}\mathrm{\forall }\alpha ,i,t$最小化$H$即可得到最优的支付排序{$x_{i,t}$}。

注意：在这个QUBO模型里，我们的第二个优化目标——最小化平均支付延迟并未出现，它是由批量大小（batch size）超参数来调整的。

3.1 超参数调整

为了能够让支付和入账抵消，我们需要积累一定数量的交易，这个数量是我们可以优化的超参数——批量大小（batch size）。

选择这个超参数需要平衡我们的两个优化目标——最小化流动性成本和最小化平均支付延迟。一方面随着批量大小的增加，可能的支付重新排序组合数量也会增长，支付和入账的抵消也就越充分，从而带来更大的流动性效率提升；但另一方面较大的批量大小也意味着需要更长的时间来积累支付进入批量（与批次数量大致呈线性关系），并且排序的处理时间也会增加。

3.2 实验数据

随机抽取了2015年1月到2017年12月期间加拿大LVTS结算数据中的30天，为了测试量子优化器在高交易量日的效果，实验数据确保在30天随机样本中包含了10天高交易量的日子。

在这30天中，使用早上8点到下午6点之间的非紧急支付请求，每个工作日大约有23,000笔交易。

4. 实验效果

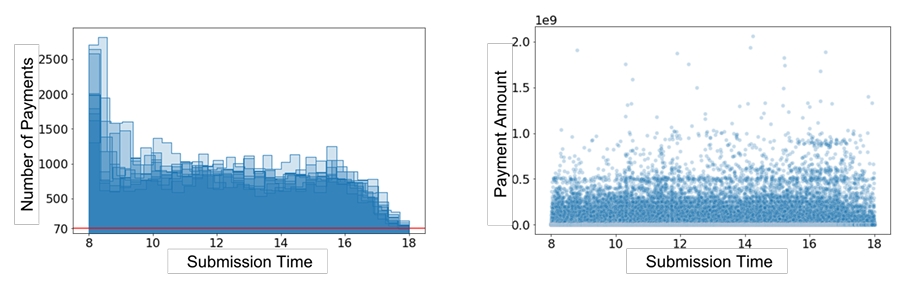（左）展示样本中每天随时间推移提交至系统的支付数量，（右）为对应的支付金额

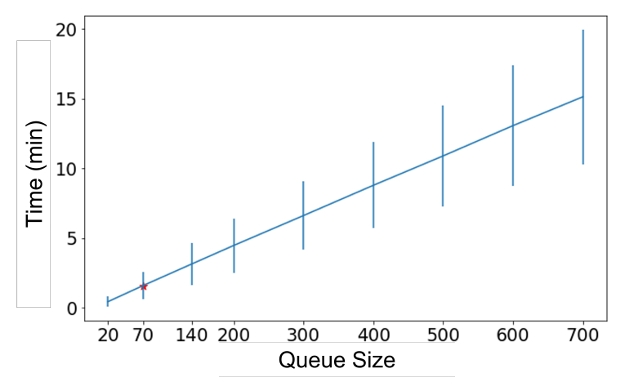给定队列容量下填满队列的平均等待时间，橙色突出显示了队列容量为70笔支付的情况

• 在多种队列大小的测试中，70笔支付的批量大小在优化流动性节约和最小化结算延迟之间达到了平衡。在该批量大小下，可以发现26%的批次实现了流动性节约，平均每日节约流动性达2.4亿加元。在样本中的一半天数里，流动性节约超过1.07亿加元，而在其中三天里，更是达到了9.97亿加元；
• 平均而言，额外的结算延迟为90秒，这个延迟主要来源于积累70笔支付所需的时间导致，而算法本身的运行时间仅为5秒；
• 为了测试不同批量大小的能力，作者在样本中选择了两个典型日，并使用140笔支付的批量运行该算法。在这些天，结果实现了显著更高的流动性节约（相比70笔支付的批量，分别多节约3.26亿加元和9400万加元），而平均每批的结算延迟为180秒（主要用于积累140笔支付）。这表明，该算法更主要的限制因素可能是积累更大批量支付所需的时间。

5. 总结：量子vs.经典

本文使用了一个不知名的开源混合整数优化器SCIP，据称类似于CPLEX，但是求解效果很差，根据提交的交易集、网络图的结构以及mNDP的下界，通常需要超过2小时才能解决，并且对于70的批次大小，在R5.4xlarge AWS实例（16个vCPU，3.1GHz，128GB内存）上运行时，有时会在超过24小时后失败。

与简单的FIFO （First-In-First-Out）排序规则比较，D-wave的CQM量子经典混合优化器在不超过250个的批次大小上基本都取得了更好的结果（更差的情况只发生在9,717个批次中的7次，且在任何一天都不会发生超过一次），超过250个的批次大小，D-wave的求解器无法在规定计算时间内获得任何可行解。

论文链接：Improving the Efficiency of Payments Systems Using Quantum Computing